SUMMARY
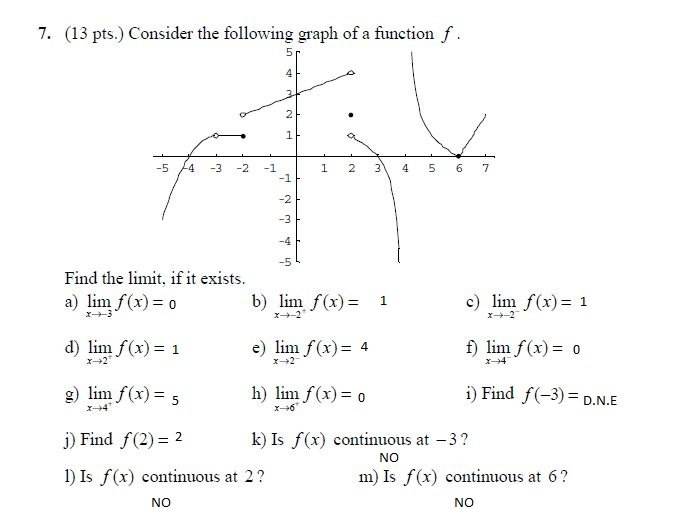
This discussion focuses on understanding limits in calculus, specifically how to determine if a limit exists from a graph. The user struggles with interpreting limits as x approaches specific values, particularly -2 and 2, and seeks clarification on the notation used. Key points include the importance of analyzing the graph from the right and left sides of the limit points, with specific limits identified as lim_{x \to -2^+} f(x) and lim_{x \to 2^-} f(x). The user is encouraged to explain their reasoning for better guidance.
PREREQUISITES
- Understanding of basic calculus concepts, particularly limits
- Familiarity with graph interpretation in calculus
- Knowledge of limit notation, including one-sided limits
- Ability to analyze function behavior near specific points
NEXT STEPS
- Study the concept of one-sided limits in calculus
- Learn how to graph functions and identify limits visually
- Practice problems involving limits approaching from both sides
- Explore the epsilon-delta definition of limits for deeper understanding
USEFUL FOR
Students studying calculus, particularly those struggling with the concept of limits and graph interpretation. This discussion is beneficial for anyone looking to improve their understanding of limit behavior in mathematical functions.