pat666
- 703
- 0
Mathematica Disagrees with ME!
(2xy-5)dx+(x^2+y^2)dy=0 y(3)=1
Ive solved this by hand and now where required to get Mathematica to solve to.
My solution: -17/3=x^2y-5x+y^3/3
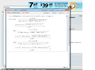
I've attached what mathematica has done. Now the question
Am I wrong ?
Is my code wrong?
Is mathematica wrong?
Thanks
P.S I rearranged to this form to sick in mathematica:
dy/dx=(-2xy+5)/(x^2+y^2)
Homework Statement
(2xy-5)dx+(x^2+y^2)dy=0 y(3)=1
Homework Equations
The Attempt at a Solution
Ive solved this by hand and now where required to get Mathematica to solve to.
My solution: -17/3=x^2y-5x+y^3/3
I've attached what mathematica has done. Now the question
Am I wrong ?
Is my code wrong?
Is mathematica wrong?
Thanks
P.S I rearranged to this form to sick in mathematica:
dy/dx=(-2xy+5)/(x^2+y^2)