MATLAB - Image Processing - Douday's rabbit fractal

[GreenPrint]

Homework Statement

13.2 A quadratic Julia set has the form

z(n+1)=z(n)^2+c

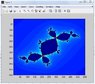
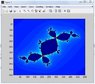
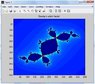
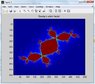
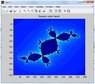
The special case where c=-.123+.745i is called Douday's rabbit fractal. Follow example 13.1, and create an image using this value of c. For the Madelbrot image, we started with all z-values equal to 0. You'll need to start with z=x+yi. Let both x and y vary from -1.5 to 1.5.

Homework Equations

The Attempt at a Solution

I'm really confused by this question. Here's my attempt at a solution. I really hope someone can point me in the right direction. My book did a very bad explaining the matter.

>> iterations=80;
grid_size=500;
[x,y]=meshgrid(linspace(-1.5,1.5,grid_size),linspace(-1.5,1.5,grid_size));
c=-.123+.745*i;
z=x+y*i;
map=x+y*i;
for k=1:iterations
    z=z.^2+c;
    a=find(abs(z)>sqrt(5));
    map(a)=k;
end
figure(1)
image(map)
colormap(jet)
? Error using ==> image
Error using ==> image
Image CData can not be complex

 

[GreenPrint]

Should I have posted this in the calculus and beyond section?

 

[Fahad Latif]

Hi,
Does anybody has idea about lbp(local binary pattern)?

 

[GreenPrint]

No sorry I don't.

 

[GreenPrint]

I feel less bad for not knowing how to solve this problem lol

 

[Fahad Latif]

I'm serious.

 

[GreenPrint]

So am I have no clue.

 

[uart]

Hi Greenprint. Your immediate problem is in this line, "map=x+y*i;".

You have a secondary problem, that will cause your printout to be monochrome (but otherwise correct) in the code related to "map(a)=k;"

But work on the immediate problem first. Can you think of a better way to initialize the map?

 

[GreenPrint]

I'm glad I ran into someone who's familiar with this topic, I guess there aren't many. This problem was my first exposure to Mandelbrot sets and of the such and my book didn't do that great of a job explaining this subject matter in the least.

Simply removing "map=x+y*i;" does seem to produce a result. I don't know why I included that in there. I used the example in my book as a guide as I'm sort of lost on this subject.

This seems to produce a image like you suggested.

iterations=80;
grid_size=500;
[x,y]=meshgrid(linspace(-1.5,1.5,grid_size),linspace(-1.5,1.5,grid_size));
c=-.123+.745*i;
z=x+y*i;
for k=1:iterations
    z=z.^2+c;
    a=find(abs(z)>sqrt(5));
    map(a)=k;
end
figure(1)
image(map)
colormap(jet)

%Example 13.1 Mandelbrot Image
clear, clc
iterations = 80;
grid_size=500;
[x,y]=meshgrid(linspace(-1.5,1.0,gird_size),linspace(-1.5,1.5,grid_size));
c=x+i*y;
z=zeros(size(x));           %set the intial matrix to 0
map=zeros(size(x));         %create a map of all grid points equal to 0
for k=1:iterations
    z=z.^2+c;
    a=find(abs(z)>sqrt(5)); %Determine which elements have exceeded sqrt(5)
    map(a)=k;
end
figure(1)
image(map)                  %Create an image
colormap(jet)

I did some more research on Mandelbrot images and must say that it's a rather fascinating topic. I have a better understanding of what exactly Mandelbrot images are but as far as creating them, not so much. I will see if I can dissect this some, as far as initializing the map, no clue.

 

[GreenPrint]

iterations=80;
grid_size=500;
[x,y]=meshgrid(linspace(-1.5,1.5,grid_size),linspace(-1.5,1.5,grid_size));
c=-.123+.745*i;
z=x+y*i;
map=zeros(size(x));
for k=1:iterations
    z=z.^2+c;
    a=find(abs(z)>sqrt(5));
    map(a)=k;
end
figure(1)
image(map)
colormap(jet)

Don't know if it's right or not.

 

[GreenPrint]

http://mathworld.wolfram.com/DouadysRabbitFractal.html
It would appear as if it's correct. It's just my image is rotated a bit I guess lol. If I wanted to label the axises, whatever the plural form of axis is, what exactly would I put for labels. I can't seem to find a similar plot with labels.

 

[uart]

"Simply removing "map=x+y*i;" does seem to produce a result"

Yeah you don't really want to just remove it. You want to initialize it with all zeros.

 

[uart]

"Don't know if it's right or not."

Yes that looks right, but I don't know how you're getting more than two color levels. There is still a mistake near the line "map(a)=k" that will cause it to constantly overwrite parts of the map that have a lower "k" value with whatever the largest value of "k" is. Effectively giving you only a monochrome image.

Perhaps the map initialization problem (failure to initialize) is masking the other problem.

 

[GreenPrint]

I'm not exactly sure.

z=x+y*i;
map=zeros(size(x));

My best bet is that there's something wrong with these lines, the only reason why I did "map=zeros(size(x))" was because it is what the example had in their problem, but that was when z was set equaled to the same exact vector. In the example they are essentially setting the map = z but doing so with my code doesn't produce any results.

Something tells me that instead of setting the map equal to k in the loop I'm suppose to use k for some other aspect like
z(k)=z.^2+c;
z(k)=z(k).^2+c;
z=z(k).^2+c;
but an image is not produce with either of these options

Something seems weird about imputing a into the map function map(a)=k;

I'm really unsure...

 

[GreenPrint]

iterations=80;
grid_size=500;
[x,y]=meshgrid(linspace(-1.5,1.5,grid_size),linspace(-1.5,1.5,grid_size));
c=-.123+.745*i;
z=x+y.*i;
map=zeros(grid_size,grid_size);
for k=1:iterations
    z=z.^2+c;
    a=find(abs(z)>sqrt(5));
    map(a)=k;
end
figure(1)
image(map)
title('Douday''s rabbit fractal')
colormap(jet)

Is this better?

 

[uart]

Yeah that's good. And are you getting a monochrome (two tone) fractal now?

 

[GreenPrint]

Yes. I'm oddly getting the same image that I did before I made the change.

Also what exactly would be the proper x and y labels on these types of graphs?

 

[uart]

Yes. I'm oddly getting the same image that I did before I made the change.

Also what exactly would be the proper x and y labels on these types of graphs?

for k=1:iterations
    z=z.^2+c;
    a=find(abs(z)>sqrt(5));
    map(a)=k;

Once abs(z) exceeds sqrt(5) on one iteration, it will exceed sqrt(5) on every subsequent iteration. Do you agree?

So the set of all points where |z|>sqrt(5) at a given iteration level "k" is a superset of that from all previous iterations. Do you agree?

So that section of your code keeps overwriting previously written elements of "map" with newer larger values of "k". This means that in the end "map" only has two levels, zero (or whatever map was initialized with) and the final value of "k". That's the reason that I think your map can only be monochrome. Are you sure you haven't changed the code subtly and not told us? Like changing the ">" for "<" for example (hint hint).

 

[GreenPrint]

No I did not accidentally change a thing

iterations=80;
grid_size=500;
[x,y]=meshgrid(linspace(-1.5,1.5,grid_size),linspace(-1.5,1.5,grid_size));
c=-.123+.745*i;
z=x+y*i;
map=zeros(size(x));
for k=1:iterations
    z=z.^2+c;
    a=find(abs(z)>sqrt(5));
    map(a)=k;
end
figure(1)
image(map)
colormap(jet)

both codes produce the same exact image, at least from what I can see

iterations=80;
grid_size=500;
[x,y]=meshgrid(linspace(-1.5,1.5,grid_size),linspace(-1.5,1.5,grid_size));
c=-.123+.745*i;
z=x+y.*i;
map=zeros(grid_size,grid_size);
for k=1:iterations
    z=z.^2+c;
    a=find(abs(z)>sqrt(5));
    map(a)=k;
end
figure(1)
image(map)
title('Douday''s rabbit fractal')
colormap(jet)

you can copy and paste and run both codes for yourself

and yes I agree to both statements

your suggested code produces the same results except the inside is colored red instead of black

iterations=80;
grid_size=500;
[x,y]=meshgrid(linspace(-1.5,1.5,grid_size),linspace(-1.5,1.5,grid_size));
c=-.123+.745*i;
z=x+y.*i;
map=zeros(grid_size,grid_size);
for k=1:iterations
    z=z.^2+c;
    a=find(abs(z)<sqrt(5));
    map(a)=k;
end
figure(1)
image(map)
title('Douday''s rabbit fractal')
colormap(jet)

Is that what you meant by monochrome?

 

[uart]

No I did not accidentally change a thing

- your suggested code produces the same results except the inside is colored red instead of black

- Is that what you meant by monochrome?

Yes that's monochrome, it basically means there are only two colors (as in a single color foreground and single color background).

The image you showed in your attachment at reply #10 in this thread was not just black and red though, it had multiple colors and shades. It was from this that I couldn't understand how your code was producing those results. Can you explain where the results in the mentioned attachment can from?

 

[GreenPrint]

Done Editing This Post =)

code #1: see attachment #1 of this post

iterations=80;
grid_size=500;
[x,y]=meshgrid(linspace(-1.5,1.5,grid_size),linspace(-1.5,1.5,grid_size));
c=-.123+.745*i;
z=x+y*i;
map=zeros(size(x));
for k=1:iterations
    z=z.^2+c;
    a=find(abs(z)>sqrt(5));
    map(a)=k;
end
figure(1)
image(map)
colormap(jet)

code #2: see attachment #2 of this post

iterations=80;
grid_size=500;
[x,y]=meshgrid(linspace(-1.5,1.5,grid_size),linspace(-1.5,1.5,grid_size));
c=-.123+.745*i;
z=x+y.*i;
map=zeros(grid_size,grid_size);
for k=1:iterations
    z=z.^2+c;
    a=find(abs(z)>sqrt(5));
    map(a)=k;
end
figure(1)
image(map)
title('Douday''s rabbit fractal')
colormap(jet)

code #3: see attachment #3 of this post

iterations=80;
grid_size=500;
[x,y]=meshgrid(linspace(-1.5,1.5,grid_size),linspace(-1.5,1.5,grid_size));
c=-.123+.745*i;
z=x+y.*i;
map=zeros(grid_size,grid_size);
for k=1:iterations
    z=z.^2+c;
    a=find(abs(z)<sqrt(5));
    map(a)=k;
end
figure(1)
image(map)
title('Douday''s rabbit fractal')
colormap(jet)

If your asking me to explain the results of the first two codes. I can't really. I just followed the example in my textbook. While my actual understanding of this topic in general is sufficient to understand the topic. I was completely lost in coming up with the code. If it wasn't for the example in my textbook I wouldn't have come up with one. I have no idea why the first two codes come up with the results that they do.

code 4: This is the example from my text
the results for the example are after the code

%Example 13.1 Mandelbrot Image
clear, clc
iterations = 80;
grid_size=500;
[x,y]=meshgrid(linspace(-1.5,1.0,grid_size),linspace(-1.5,1.5,grid_size));
c=x+i*y;
z=zeros(size(x));           %set the intial matrix to 0
map=zeros(size(x));         %create a map of all grid points equal to 0
for k=1:iterations
    z=z.^2+c;
    a=find(abs(z)>sqrt(5)); %Determine which elements have exceeded sqrt(5)
    map(a)=k;
end
figure(1)
image(map)                  %Create an image
colormap(jet)

THIS IS FOR CODE 4
[PLAIN]http://img20.imageshack.us/img20/7077/capture4pu.jpg
THIS IS FOR CODE 4

Just out of curiosity. If i were to label the x and y axes on these figures what would be the proper labels?

The above codes and corresponding attachments match correctly with their code. Note that code 4 results weren't stored as a attachment but the rest were.

 

[uart]

There is no functional difference between the first two code examples. "map=zeros(size(x))" and "map=zeros(grid_size,grid_size)" do exactly the same thing in this context. There is absolutely no reason to expect any output differences there, you can flip a coin on which method you use to initialize the map to zero.

While my actual understanding of this topic in general is sufficient to understand the topic. I was completely lost in coming up with the code. If it wasn't for the example in my textbook I wouldn't have come up with one. I have no idea why the first two codes come up with the results that they do.

The thing you're trying to plot is the set of all starting points $z_0$, in the complex plane, for which the iterative process of z=z^2+c (starting with z=z0) remains bounded. The thing you're calculating in "map" is essentially an "indicator function" for the set. That is, a function that is zero if the point is not in the set and one if the point is in the set (or actually in this case two values that are not necessarily zero and one, but essentially the same thing).

So for the basic set you really only get a two color map with this type of thing (same for the mandelbrot set). People however often like to get something that looks a bit more interesting than just two colors. So instead of using just one value for "in the set" and one other value for "not in the set", they still use just one color for "in the set" but for "not in the set" they use a number proportional to (or in some other way related to) the number of iterations taken for the point to "escape" to some predefined radius. (this is some radius from which divergence is inevitable).

Yes I've ran your code in gnu-octave (a freeware MATLAB clone) and it produces exactly what I expected, a two level map containing only 0's and 80's. I have no idea how you are getting shades and colors there from a two level map.

Just out of curiosity. If i were to label the x and y axes on these figures what would be the proper labels?

Properly scaled they are the real and imaginary values of points in the complex plane, that is Re(z) and Im(z). As they are currently drawn they are approximately ( Re(z) + 1.5 )*500/3 and ( Im(z) + 1.5 )*500/3 respectively.

 

[GreenPrint]

http://imageshack.us/clip/my-videos/193/fpx.mp4/

iterations=80;
grid_size=500;
[x,y]=meshgrid(linspace(-1.5,1.5,grid_size),linspace(-1.5,1.5,grid_size));
c=-.123+.745*i;
z=x+y.*i;
map=zeros(grid_size,grid_size);
for k=1:iterations
    z=z.^2+c;
    a=find(abs(z)>sqrt(5));
    map(a)=k;
end
figure(1)
image(map)
title('Douday''s rabbit fractal')
colormap(jet)

 

[uart]

First attachment : Here's what I get from your code.

Second attachment : And here's what I get if I replace "abs(z) > .." with "abs(z) < .." as I suggested.

So pretty much exactly as I predicted.

 

[GreenPrint]

make sure you click on the full screen button
i can't post videos so i just posted a link to it on imageshack in the previous post

 

[GreenPrint]

Well this wouldn't be the first time my copy of MATLAB has been doing things other peoples didn't. Have you seen my topic about floating point numbers? >_> somebody runs the same exact code that I do on MATLAB that stresses the difference on how to find the exact answer versus a rounded answer when solving a function and he gets both. My copy of MATLAB only produces two estimated answers =_=.

 

[uart]

Yeah that's strange. Can you take a look at the numbers stored in "map". I would have expected it be only zero's and 80's

There may be some differences in the way gnu-Octave and Matlab handles the "image" command to actually render the map, but I can't see any way the it should produce a different "map" matrix.

So take a look at the data in the "map" matrix and see if it's all zero's and 80's or if are there other numbers in there as well.

BTW. Can someone else running Matlab chime in here and check GreenPrints code?

 

[GreenPrint]

I copied and pasted the 500x500 array that was stored in "map"

"beetxt.com/apz"[/URL]

I don't think that's all of it >_> but like the first couple hundred characters but that should give you an idea of what was stored in "map"

I can upload the actual file itself if you want or something

 

[uart]

Yes that's definitely a multi-level map (and therefore consistent with the multi-color multi-tone image being displayed).

Could you try one more thing just for interest. Could you try replacing,

 a = find(abs(z)>sqrt(5));

with

 a = (abs(z)>sqrt(5));

It should give exactly the same results. Basically it changes the way that MATLAB stores the information in "a" from a linear array (which has advantages of sparsity) to a logical matrix of the same dimensions as the map.

The second method might use a little more memory but it is simpler and definitely more transparent, so it would be interesting if you could give that a try. Both of the above give identical results for me on gnu-Octave, (both of which are different to your results as previously stated).

 

[GreenPrint]

Code #1

iterations=80;
grid_size=500;
[x,y]=meshgrid(linspace(-1.5,1.5,grid_size),linspace(-1.5,1.5,grid_size));
c=-.123+.745*i;
z=x+y.*i;
map=zeros(grid_size,grid_size);
for k=1:iterations
    z=z.^2+c;
    a=find(abs(z)>sqrt(5));
    map(a)=k;
end
figure(1)
image(map)
title('Douday''s rabbit fractal')
colormap(jet)

See attachment #2 in post #21

Code #2

iterations=80;
grid_size=500;
[x,y]=meshgrid(linspace(-1.5,1.5,grid_size),linspace(-1.5,1.5,grid_size));
c=-.123+.745*i;
z=x+y.*i;
map=zeros(grid_size,grid_size);
for k=1:iterations
    z=z.^2+c;
    a = (abs(z)>sqrt(5));
    map(a)=k;
end
figure(1)
image(map)
title('Douday''s rabbit fractal')
colormap(jet)

See attachment #1 in this post

Interesting their identical to each other.