- #1
saadhusayn
- 22
- 1
Say we have a matrix [itex]L[/itex] that maps vector components from an unprimed basis to a rotated primed basis according to the rule [itex]x'_{i} = L_{ij} x_{j}[/itex]. [itex]x'_i[/itex] is the [itex]i[/itex]th component in the primed basis and [itex]x_{j}[/itex] the [itex]j[/itex] th component in the original unprimed basis. Now [itex]x'_{i} = \overline{e}'_i. \overline{x} = \overline{e}'_i. \overline{e}_j x_{j} [/itex]. Hence [itex]L_{ij} = \overline{e}'_i. \overline{e}_j[/itex]. Thus the matrix equation relating the primed co-ordinate system to the unprimed one in [itex]\mathbb{R}^3[/itex] is
$$ \begin{pmatrix}x'_{1}\\ x'_{2}\\ x'_{3} \end{pmatrix} = \begin{pmatrix} \overline{e}'_1. \overline{e}_1 & \overline{e}'_1. \overline{e}_2 & \overline{e}'_1. \overline{e}_3\\ \overline{e}'_2. \overline{e}_1 & \overline{e}'_2. \overline{e}_2 & \overline{e}'_2. \overline{e}_1 \\ \overline{e}'_3. \overline{e}_1 & \overline{e}'_3. \overline{e}_2 & \overline{e}'_3. \overline{e}_3 \end{pmatrix}\begin{pmatrix}x_{1}\\ x_{2}\\ x_{3} \end{pmatrix} $$
Where the [itex]\overline{e}'_i[/itex]s and [itex]\overline{e}_j[/itex]s are unit basis vectors in the primed and unprimed co ordinate systems respectively.
Now I tried to apply the above idea to the following situation (Riley, Hobson and Bence Chapter 26, Problem 2).
I took [itex]\mathbf{A} = \overline{e}_1[/itex] and [itex]\mathbf{B} = \overline{e}_2[/itex]. It turns out that the matrix that transforms [itex]\mathbf{A} \rightarrow \mathbf{A}' [/itex] and [itex]\mathbf{B} \rightarrow \mathbf{B}' [/itex] is not the matrix that transforms the unprimed components to the primed components (that I used above) but the INVERSE (or transpose) of that matrix. I need to know where I am going wrong here. Thank you.
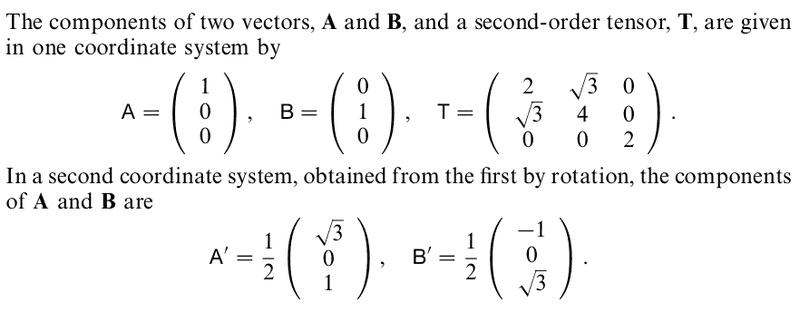
$$ \begin{pmatrix}x'_{1}\\ x'_{2}\\ x'_{3} \end{pmatrix} = \begin{pmatrix} \overline{e}'_1. \overline{e}_1 & \overline{e}'_1. \overline{e}_2 & \overline{e}'_1. \overline{e}_3\\ \overline{e}'_2. \overline{e}_1 & \overline{e}'_2. \overline{e}_2 & \overline{e}'_2. \overline{e}_1 \\ \overline{e}'_3. \overline{e}_1 & \overline{e}'_3. \overline{e}_2 & \overline{e}'_3. \overline{e}_3 \end{pmatrix}\begin{pmatrix}x_{1}\\ x_{2}\\ x_{3} \end{pmatrix} $$
Where the [itex]\overline{e}'_i[/itex]s and [itex]\overline{e}_j[/itex]s are unit basis vectors in the primed and unprimed co ordinate systems respectively.
Now I tried to apply the above idea to the following situation (Riley, Hobson and Bence Chapter 26, Problem 2).
I took [itex]\mathbf{A} = \overline{e}_1[/itex] and [itex]\mathbf{B} = \overline{e}_2[/itex]. It turns out that the matrix that transforms [itex]\mathbf{A} \rightarrow \mathbf{A}' [/itex] and [itex]\mathbf{B} \rightarrow \mathbf{B}' [/itex] is not the matrix that transforms the unprimed components to the primed components (that I used above) but the INVERSE (or transpose) of that matrix. I need to know where I am going wrong here. Thank you.