Maximising an area - goat in field

[lavster]

Homework Statement

this isn't a homeowrk question as such - its a question that my Grandpa asked me.

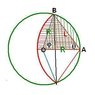
You have a circular field, and a goat tied up to a post which is somewhere on the cirumference of the field. How long does is the rope if the goat is able to eat exactly half of the grass in the field

Homework Equations

area of field = pi * r^2, and say for arguments sake that the radius of the field is 10 meters. let r be radius of field and R be radius goats rope

The Attempt at a Solution

I thought that you would maximise by differentiating at first, or solving a quadratic but unsuprisingly its not that simple!

 

[ehild]

What about a nice drawing of the field with grass and goat and string? It would show how to solve this problem.

ehild

 

[HallsofIvy]

What you are really asking about is the area of the intersection of two circles. Let's take the field to be a circle of radius R. The region the goat can eat the portion of a circle of radius r with center on the circumference of the first circle that is contained within the circle. I would be inclined to do this as coordinate geometry: Set up a coordinate system so that the first circle has center at the origin, take the center of the second circle to be at (0, R) and write the equations of both circles. You might need to integrate to find the area of the intersection in terms of r and R. Then set that equal to $\pi R^2/2$ and solve for r.

 

[ehild]

Here is a picture... The shaded area is R²π/4, and it is the sum of two circle sectors minus the area of the triangle OAB. No need of calculus, but the equation to be solved is rather ugly.

ehild