Maximizing Horizontal Range of a Projectile

[neilparker62]

Introduction
A recent homework problem that appeared in the forums was concerned with maximizing the horizontal range of a projectile subject to the launch site being a fixed height above the ground upon which the projectile eventually impacted. A number of interesting methods of solution arose so the idea of this article is to present all of these since each method illustrates a different approach to the problem and each is instructive in its own right.
The Problem
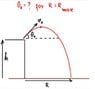
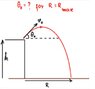
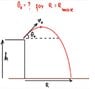
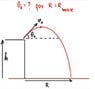
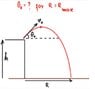
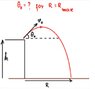
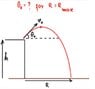
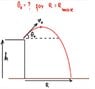
A cannon sits on top of a plane at a height $h$ above the ground and fires a shell with an initial velocity $v_0$. At what angle $\theta_0$ must it fire the shell to attain maximum range $R_{\text{max}}$ along the ground?
I hope the OP (original poster) of the above problem will not mind me including his problem diagram:

Parametric Equations
The above motion may be represented by the following pair of...

Continue reading...

 

[jedishrfu]

Nice article! Thanks for writing and sharing it!

 

[aabottom]

Thanks for posting. An error, perhaps, and a question, I extend. 1] In the 3rd equation right hand side, the first term should be $$R~tan(\theta)$$ and NOT $$v_0~R~tan(\theta) ~.$$ 2] In Method 2, should your definitions of $\alpha$ be $$sin(\alpha) = \frac{h}{R'} , where $$ $$R' = \sqrt{h^2+R^2}~,$$ and $R$ is defined as in your figure?

 

[neilparker62]

Thanks for the correction - have updated as per your suggestion. Please let me know if there's anything still unclear.

 

[neilparker62]

I attempted solving this problem using @kuruman 's equation $|\vec{v_i} \times \vec{v_f}|=Rg$ in Method 3. Wolfram Alpha choked on it - readers might find it interesting to figure out why ?

 

[kuruman]

I am a Mathematica person myself so I put the two kinematic equations in x and y and asked it to solve for the time of flight tf and the height h. It worked fine (see below). I don't understand WA code well enough to ascertain what you are doing with it.

 

[neilparker62]

Don't go conventional - just trust your own method! WA choked and it wasn't because your method or WA is at fault! The 'code' I put in was quite simple - it asked WA to solve the vector equation directly. What you have above is the solution provided on the kinematics webpage here and your vector technique shows it up as wrong!

 

[kuruman]

Don't go conventional - just trust your own method! WA choked and it wasn't because your method or WA is at fault! The 'code' I put in was quite simple - it asked WA to solve the vector equation directly. What you have above is the solution provided on the kinematics webpage here and your vector technique shows it up as wrong!

I don't see why the WA 'code' is a vector equation. I can see the two-dimensional vector on the left side but the right-hand side looks like a scalar and why is it negative? Also, I don't know about WA, but Mathematica does not accept 2-d vector cross products. For 2-d vectors, a third component must be set to zero.

I think the proper way to use the equation directly in WA is to ask it to solve the equation $$\sqrt{\left[v_0(\cos\theta, \sin\theta,0) \times (v_0\cos\theta,-\sqrt{v_{0}^2\sin^2\theta-2g\Delta h},0)\right]\cdot \left[v_0(\cos\theta, \sin\theta,0) \times (v_0\cos\theta,-\sqrt{v_{0}^2\sin^2\theta-2g\Delta h},0)\right]} =gR.$$The LHS is the square root of the dot product of the cross product with itself, i.e. the magnitude. It is set equal to $gR$, a positive quantity.

I tried this with Mathematica. The numerical NSolve befuddled it. However, I got the expected result with cautionary messages when I used FindRoot and gave it an approximate value for $\Delta h$.

 

[neilparker62]

WA is fine with 2D vector cross products. eg (ai + bj) x (ci + dj) would be entered as {a,b} cross {c,d}. The output is negative because i x -j is negative. On entry you need to make sure the $v_f$ vector is pointing downwards because the projectile is landing on the roof. It has passed (or should have passed) the maximum point of the trajectory. The reason WA chokes is not because it is wrong nor that your vector equation is wrong but because 15m is on the wrong side of the axis of symmetry - the projectile is still heading upward at that point. See following parametric graph of the projectile motion:

https://www.desmos.com/calculator/fwage30bpg