Maximizing radiation southward, minimizing it northward, antennas

[PhDeezNutz]

Homework Statement

More of a conceptual question than a homework question. Maximizing radiation southward and minimizing it northward.

Relevant Equations

(See picture in attempt at solution)

For two antennas separated along the north-south direction, operating with the same amplitude $E_0$, same wavelength $\lambda$, separated by a distance $d$, and with a phase difference $\delta$ the formula for radiated intensity is

$$I = 4I_0 \cos^2 \left(\pi \frac{d}{\lambda}\sin \theta + \frac{\delta}{2} \right)$$

Homework Statement: More of a conceptual question than a homework question. Maximizing radiation southward and minimizing it northward.
Homework Equations: (See picture in attempt at solution)

For two antennas separated along the north-south direction, operating with the same amplitude $E_0$, same wavelength $\lambda$, separated by a distance $d$, and with a phase difference $\delta$ the formula for radiated intensity is

$$I = 4I_0 \cos^2 \left(\pi \frac{d}{\lambda}\sin \theta + \frac{\delta}{2} \right)$$

I'm going off these notes

https://scholar.harvard.edu/files/schwartz/files/lecture18-antennas.pdf
which uses this picture

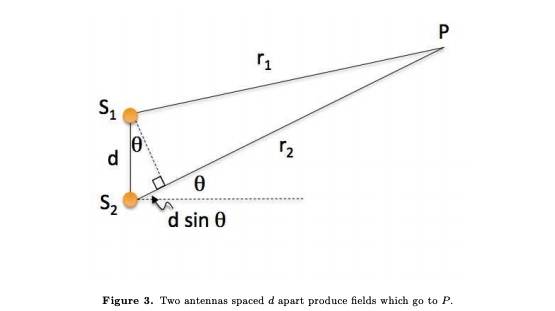
My attempt at a solution is as follows, and it seems to corroborate what they are saying. That said, I will challenge it at the end on the grounds of rotational symmetry.

At the very least we want $I\left( \theta = \frac{\pi}{2} \right) = 0$ and $I\left( \theta = \frac{3\pi}{2} \right) = 4I_0$

$$4I_0 \cos^2 \left( \pi \frac{d}{\lambda} + \frac{\delta}{2} \right) = 0$$

$$4I_0 \cos^2 \left( -\pi \frac{d}{\lambda} + \frac{\delta}{2} \right) = 0$$

Then we have

$$\pi \frac{d}{\lambda} + \frac{\delta}{2} = \frac{\pi}{2}$$

$$-\pi \frac{d}{\lambda} + \frac{\delta}{2} = 0$$

Therefore

$$\delta = \frac{\pi}{2}$$

substituting back in we find

$$d = \frac{\lambda}{4}$$

This answer corroborates their answer on the bottom of page 6/ top of page 7. Their graph is

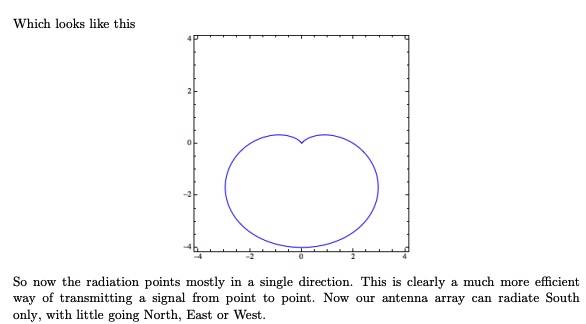
Mathematically everything checks out but I'm challenging it on physical grounds. Intuitively you think you would get the same interference pattern in both directions; If your rotate this system 180 degrees it should be the same system.

Can someone help me reconcile this?

As always, any help is appreciated.

 

[hutchphd]

The left right symmetry holds but you break the symmetry top to bottom by driving them differently.

 

[PhDeezNutz]

I’m afraid I don’t follow. If you flip the system 180 degrees you still get the same phase difference along the “top bottom axis” and I would think the same interference pattern (in both directions up and down).

To me it’s all a matter of which one you want to have phase pi/2 and which one you want to have phase 0. It shouldn’t matter which one you call which.

I’ll try doing the math explicitly for traveling waves.

Edit: also the formulation in the link doesn’t seem to mention different frequencies in their derivation.

 

[hutchphd]

Yes you need to write down the waves. When you do you will see that changing δ from plus to minus π/2 changes the preferred "polar" direction. The sign of the phase matters...

 

[PhDeezNutz]

Yes you need to write down the waves. When you do you will see that changing δ from plus to minus π/2 changes the preferred "polar" direction. The sign of the phase matters...

Thank you for your response.

Would it be alright if I just dispensed with the polar angle and just treated the problem "along the z-axis"?

 

[hutchphd]

Yes you can show the effect in 1 dimension. Two plane waves on the z axis.

 

[PhDeezNutz]

Alright here we go, I treated the problem in one dimension according to the following picture. This is just a picture, later on I will show through the math that $S_2$ should actually be located below $S_1$ (which is located at the origin) assuming $S_2$ has zero phase and we associated the phase with $S_1$.

Here's the picture; Here I'm trying to maximize radiation northwards and minimize it southward. The exact opposite of what I said in the OP.

Finding the field at P due to both sources (as drawn)

$$E_1 = E_0 e^{ikz}e^{-i\omega t}e^{i \phi}$$

$$E_2 = E_0 e^{ikz}e^{-ikd}e^{- i \omega t}$$

$$E_{total} = E_1 + E_2 = E_0 e^{ikz}e^{-i \omega t} \left(e^{i\phi} + e^{-ikd} \right)$$

$$\| E_{total} \|^2 = \left( E_0 \right)^2 \left( 2 + 2 \cos \left( \phi + kd \right)\right)$$

If we want to maximize radiation northwards (Equation 1)

$$\phi = -kd$$

Finding the field at P' due to both sources (as drawn)

$$E_1 = E_0 e^{ikz}e^{-i\omega t}e^{i \phi}$$

$$E_2 = E_0 e^{ikz}e^{ikd}e^{- i \omega t}$$ (Notice the change of sign from -ikd to ikd when we were treating the first case)

$$E_{total} = E_1 + E_2 = E_0 e^{ikz}e^{-i \omega t} \left(e^{i\phi} + e^{ikd} \right)$$

$$\| E_{total} \|^2 = \left( E_0 \right)^2 \left( 2 + 2 \cos \left( \phi - kd \right)\right)$$

If we want to minimize radiation southwards (Equation 2)

$$\phi - kd = \pi$$

Trying to reconcile Equation 1 and Equation 2 we find

$$ d = - \frac{\lambda}{4} $$

$$ \phi = \frac{\pi}{2} $$

Bringing it all together

The negative $d$ value indicates the $S_2$ should actually be located beneath $S_1$.

$$S_1 = \left( 0,0,0 \right)$$

$$S_2 = \left( 0,0, -\frac{\lambda}{4} \right)$$

$S_1$ should be operated with a phase that is $$\frac{\pi}{2}$$ behind $S_2$

Long story short

the top and bottom sources should be separated by a distance of $d = \frac{\lambda}{4}$ with the top source being operated at a phase $\frac{\pi}{2}$ behind the bottom source. Or alternatively the bottom source being operated at a phase $\frac{\pi}{2}$ ahead of the top source.

I think I got the right answer, even If I did, it still doesn't make much intuitive sense.

 

[hutchphd]

Its all here

$$E_{total} = E_1 + E_2 = E_0 e^{ikz}e^{-i \omega t} \left(e^{i\phi} + e^{-ikd} \right)$$

The quantity in () can vanish or be as large as 2.
Each source actually sends waves in both directions. If you choose the phase to make the +z wave vanish, the -z wave will be maximal and vice-versa.
No crazy physics here...but you need to get comfortable with it.