Maximum displacement of a coupled pendulum

[Astrogirl101]

Homework Statement

How are the maximum displacements of each pendulum related for ω1 and ω2? Draw a sketch that describes the motion of the system in each case

Relevant Equations

ω1 =√(g/l)
ω2=√(g/l+2k/m)

Hi,
So I have this question to solve and I have no idea how to do it.
It states: ''How are the maximum displacements of each pendulum related for ω1 and ω2? Draw a sketch that describes the motion of the system in each case. ''

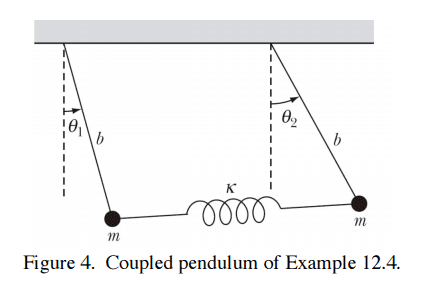
The 2 angular frequencies that I have found are ω1 =√(g/l) and ω2=√(g/l+2k/m)

 

[BvU]

Hello Astrogirl, $\qquad$ $\qquad$ !

The 2 angular frequencies that I have found are ω1 =√(g/l) and ω2=√(g/l+2k/m)

Then you must know something we don't know, because $l$ doesn't appear in the problem statement.

Please post your work ! How did you find $\omega_1$ and $\omega_2\ ?$
$\$