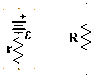Maximum power theory in electronics

[logearav]

Homework Statement

Please see my attachment. From the circuit
Energy transferred to the load E = Ir + IR, where r is the internal resistance and R is Load Resistance. so
I = E/(r+R)

Homework Equations

The Attempt at a Solution

The Power W is W = I²R = E²R/(r+R)²
Upto this i understand. I can't understand the following steps
As R changes, so does W. W will be maximum when dW/dR is zero
that is d/dR(E²R/(r+R)²) = 0
My question is why W is maximum when dW/dR = 0. Why dW/dR concept is introduced here

 

[gneill]

It's the basic calculus method for minimizing or maximizing a function. Take the derivative of the function with respect to the variable you wish to minimize (or maximize) with respect to, set the derivative equal to zero and solve for that variable. The resulting value(s) of the variable will either minimize or maximize the function.

 

[logearav]

Thanks gneill. But, can't this maximum theory be explained by any other concept other than calculus method. I can't understand this method.

 

[gneill]

Thanks gneill. But, can't this maximum theory be explained by any other concept other than calculus method. I can't understand this method.

Well, you could graph the function with respect to r and visually see the maximum

 

[logearav]

Thanks Gneill.