Mechanical energy of a block sliding on a circular path

[CGandC]

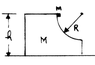
Homework Statement

( The following problem is taken from kleppner's " Introduction to mechanics" )
( The question in the book talks about the velocity but my confusion is related to the Energy )

Homework Equations

Conservation of Mechanical energy : Ef - Ei = 0
Consevation of Momentum : Pf - Pi = 0

The Attempt at a Solution

If I can assume the time which mass 'm' reaches the edge of the block is very small , and if I also assume both masses ( m , M ) are pretty small , then the total impulse can be approximately zero and the total momentum difference is conserved , so that :

where ' V ' is the velocity of the larger object 'M'
and ' v ' is the velocity of the smaller object 'm'

So far all is correct.

Afterwards , I used the total conservation of mechanical energy : Ef - Ei = 0
and only used it for mass 'm' ( the normal force does no work since it's constantly prependicular to the
cube's path and the only work done on mass 'm' is from gravity ) so that :

Eventually getting ( my answer ) :

However , this is not the correct answer , because in the answers they included both the energies by mass 'm' and mass 'M' , so that:

Eventually getting ( the correct answer ) :

So my question is : why I can't use the total consevation of mechanical energy for only mass 'm' like I did , why's it not correct? ( gravitational potential energy is included , kinetic energy is included and normal force does no work ) and why do I have to add the energies of the bigger mass ' M ' ?

 

[conscience]

( the normal force does no work since it's constantly prependicular to the
cube's path

I think the problem lies here . Isn't large block of mass M also moving ?

 

[CGandC]

I think the problem lies here . Isn't large block of mass M also moving ?

Yes, but why do I have to add it's energy? , after all , it seems that there doesn't exist some force on mass 'm1' which does work to be added into the conservation of mechanical energy of mass 'm' , in order to correct the equation:

 

[conscience]

Yes, but why do I have to add it's energy? , after all , it seems that there doesn't exist some force on mass 'm1' which does work to be added into the conservation of mechanical energy of mass 'm' , in order to correct the equation: View attachment 211579

You are incorrectly assuming that work done by normal force on small cube is zero. It isn't .

 

[CGandC]

You are incorrectly assuming that work done by normal force on small cube is zero. It isn't .

Why not? , it is perpendicular to the small cube's path .

 

[MarkFL]

It seems to me that you are neglecting conservation of momentum, which means your calculation of final energy is missing the kinetic energy of the large block.

 

[conscience]

Why not? , it is perpendicular to the small cube's path .

The path of the small cube is circular when seen from the moving frame of block M .It's path as seen from the ground frame is not circular .

V_c = V_c,M + V_M

The first term on right side is the relative velocity of cube w.r.t M . It is this component which is perpendicular to normal force . But the dot product of second component with N is not zero .

Negative work is done by normal force on small cube as it slides along the circular arc

 

[CGandC]

It seems to me that you are neglecting conservation of momentum, which means your calculation of final energy is missing the kinetic energy of the large block.

Yes , it does miss the kinetic energy of the large block but I still don't fully understand why do I need to add it, can't I just use the energies of the small cube?

and the conservation of momentum is conserved which is why I get :

 

[MarkFL]

Yes , it does miss the kinetic energy of the large block but I still don't fully understand why do I need to add it, can't I just use the energies of the small cube?

and the conservation of momentum is conserved which is why I get : View attachment 211604

Okay, so this implies:

$mv=MV\implies V=\dfrac{mv}{M}$

And so, by conservation of energy, we have:

$\Delta E=E_i-E_f=mgR-\dfrac{1}{2}\left(mv^2+MV^2\right)=0$

or:

$2mgR=mv^2+MV^2$

Using the implication from conservation of momentum, we obtain:

$2mgR=mv^2+M\left(\dfrac{mv}{M}\right)^2$

Solve for $v$...what do you get?

 

[haruspex]

can't I just use the energies of the small cube?

As conscience pointed out in post #7, the path of the small cube, seen in a rest frame, is not an arc of a circle. Its motion does have a component in the direction of the normal force. So it is not obvious what the energy of the small cube is.

 

[CGandC]

As conscience pointed out in post #7, the path of the small cube, seen in a rest frame, is not an arc of a circle. Its motion does have a component in the direction of the normal force. So it is not obvious what the energy of the small cube is.

Then suppose I'm at the frame of the moving block M , so that the path the small cube does is circular.
Then the normal force does no work and why do I still need to add the energies of the large block of mass 'M' ( to the energies of the small cube ) ?

 

[conscience]

Then suppose I'm at the frame of the moving block M , so that the path the small cube does is circular.
Then the normal force does no work

You cannot apply Work Energy theorem from a non inertial frame .Since block M is accelerating , energy conservation doesn't hold true .

As seen from block M , $mgR ≠ \frac{1}{2}mv^2$ , where v is relative speed of cube with respect to M as it meaves M .

 

[CGandC]

You cannot apply Work Energy theorem from a non inertial frame .Since block M is accelerating , energy conservation doesn't hold true .

As seen from block M , $mgR ≠ \frac{1}{2}mv^2$ , where v is relative speed of cube with respect to M as it meaves M .

So if I'm at the frame of accelerating block M , the energy conservation for the small cube will only hold if I were to introduce some pseudo-force (which will do work on the small cube in the eyes of the accelerating frame ) ?

 

[haruspex]

So if I'm at the frame of accelerating block M , the energy conservation for the small cube will only hold if I were to introduce some pseudo-force (which will do work on the small cube in the eyes of the accelerating frame ) ?

That still does not fix it. In the accelerating frame, how do you decide the displacement over which the pseudo force has acted?

 

[conscience]

So if I'm at the frame of accelerating block M , the energy conservation for the small cube will only hold if I were to introduce some pseudo-force (which will do work on the small cube in the eyes of the accelerating frame ) ?

That's right .

But the difficulty in this problem is that the block M is having varying acceleration .

Varying pseudo force

 

[haruspex]

That's right .

I don't think that introducing the pseuo force makes the energy balance work. In the accelerating frame it would appear that the force makes no advance. See post #14.

 

[conscience]

In the accelerating frame, how do you decide the displacement over which the pseudo force has acted?

In the accelerated frame M , cube m is moving in a circular arc .At any moment displacement is tangent to the path .Direction of pseudo force is also known .It's the magnitude of this pseudo force which is not constant .

I don't think that introducing the pseuo force makes the energy balance work.

Work energy theorem is certainly valid in an accelerating frame if we account for work done by pseudo force .

Work Energy theorem is a consequence of Newton's second law . If Newton's law is valid in an accelerated frame, why shouldn't Work Energy theorem be valid ?

 

[haruspex]

Work Energy theorem is a consequence of Newton's second law . If Newton's law is valid in an accelerated framw, why shouldn't Work Energy theorem be valid ?

Work done appears different in different frames. If you stand in an elevator moving up or down at different (but constant) acceleration the work done in that frame always appears to be zero.
Within that frame, there is no contradiction.

 

[conscience]

Work done appears different in different frames. If you stand in an elevator moving up or down at different (but constant) acceleration the work done in that frame always appears to be zero.
Within that frame, there is no contradiction.

No work , no change in energy .

Work Energy theorem is valid in this accelerated frame .

Note that mechanical energy is not invariant between different frames .

 

[haruspex]

No work , no change in energy .

Work Energy theorem is valid in this accelerated frame .

Note that mechanical energy is not invariant between different frames .

You are right... sorry for the noise.

 

[conscience]

sorry for the noise.

Not at all . Generally work energy theorem is not applied from an accelerated frame . So you might have found it unusual .

But I agree the more common and safe approach is to apply energy conservation from an inertial frame .