- #1
losbellos
- 63
- 0
Here in this case an arm in special constrain.
The arm is capable to rotate around the main center if force
is applied to the center. The torque practically generated by
the force that is pushing Tarm. Tamr rotates and pulls with more or less the same force at the top that horizontal force then converted to rolling on the surface. So that would be a normal force and the remaining component that would roll the whole system.
The Two red arrow means that the force is created at the bottom and the top "exactly" the same would be
My question would be that how much is the torque from C point perspective?
I wasn't able to calculate out because PC is a constraint that is not stationary. Can anybody help on this?
Green parts are stationary.
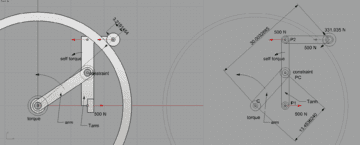
The arm is capable to rotate around the main center if force
is applied to the center. The torque practically generated by
the force that is pushing Tarm. Tamr rotates and pulls with more or less the same force at the top that horizontal force then converted to rolling on the surface. So that would be a normal force and the remaining component that would roll the whole system.
The Two red arrow means that the force is created at the bottom and the top "exactly" the same would be
My question would be that how much is the torque from C point perspective?
I wasn't able to calculate out because PC is a constraint that is not stationary. Can anybody help on this?
Green parts are stationary.
Last edited: