Metal Strip Magnetic Field question

AI Thread Summary
A metal strip measuring 7.50 cm by 0.550 cm and 0.800 mm thick moves through a magnetic field of 1.00 mT, generating a potential difference of 3.90 µV. The discussion focuses on calculating the speed of the strip using the formula v = V/(Bd). An error was identified in the initial calculations due to using an incorrect value for the thickness (d). Correcting this value is crucial for accurately determining the speed. The conversation emphasizes the importance of using the right parameters in magnetic field calculations.
tigert2004
Messages
7
Reaction score
0
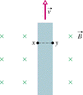
A metal strip 7.50 cm long, 0.550 cm wide, and 0.800 mm thick moves with constant velocity v through a magnetic field B = 1.00 mT pointing perpendicular to the strip, as shown in Figure 28-35. A potential difference of 3.90 µV is measured between points x and y across the strip. Calculate the speed v

I am getting since vd =i/neA and then replace n by Bi/Vle equaling Vl/BA then since l= A/d you get V/Bd But that does not give me the right answer
 

Attachments

  • hrw7_28-35.gif
    hrw7_28-35.gif
    2.4 KB · Views: 872
Last edited:
Physics news on Phys.org
I realized what I was doing wrong. I was using the wrong value for d
 

Thread 'Rolling without slipping on a curved surface'

Kindly see the attached pdf. My attempt to solve it, is in it. I'm wondering if my solution is right. My idea is this: At any point of time, the ball may be assumed to be at an incline which is at an angle of θ(kindly see both the pics in the pdf file). The value of θ will continuously change and so will the value of friction. I'm not able to figure out, why my solution is wrong, if it is wrong .
View full post »

Thread 'Struggling to understand the concept of this question (ice cube in water optics question)'

TL;DR Summary: I came across this question from a Sri Lankan A-level textbook. Question - An ice cube with a length of 10 cm is immersed in water at 0 °C. An observer observes the ice cube from the water, and it seems to be 7.75 cm long. If the refractive index of water is 4/3, find the height of the ice cube immersed in the water. I could not understand how the apparent height of the ice cube in the water depends on the height of the ice cube immersed in the water. Does anyone have an...
View full post »

Similar threads

Solve Magnetic Field Homework: Find Velocity of Metal Strip
Replies
1
Views
2K
Hall effect/force on current carrying wire
Replies
11
Views
2K
Magnetic field at a point above a metal strip.
Replies
15
Views
7K
Hall Effect Probe for Measuring Magnetic Field Strength
Replies
1
Views
5K
How Is Current Calculated in a Mass Spectrometer?
Replies
3
Views
2K
A strip of copper placed in a magnetic field
Replies
5
Views
5K
Magnetic field in the case of a thin magnetized cylinder
Replies
11
Views
2K
How Do You Calculate Terminal Velocity of a Metal Ring in a Magnetic Field?
Replies
3
Views
2K
Magnitude of the induced magnetic field in a circuit
Replies
5
Views
4K
Circular loop in magnetic field
Replies
6
Views
5K

Hot Threads

Recent Insights

Back
Top