Akhilesh Prasad
- 4
- 0
1. Prolem Statement:-
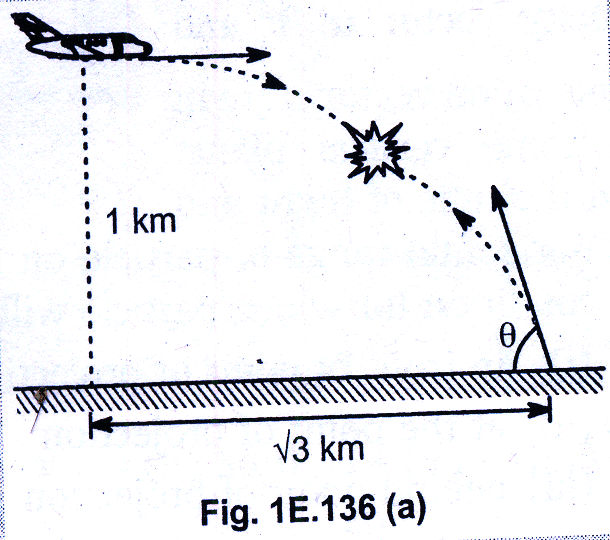
An aircraft is flying horizontally with constant velocity = ##200 m/s##, at a height = ##1 km## above the ground. At the moment shown, a bomb is released from aircraft and the canon- gun below fires a shell with initial speed = ##200 m/s##, at some angle #\theta#.
1)For what value of ##'\theta'## will the projectile shell destroy the bomb in mid- air ? If the value of ##'\theta'## is ##53^{\circ}##.
2)Find the minimum distance between the bomb and the shell as they fly past each other. Take ##\sin53^{\circ}=4/5##.
The figure for the question is as shown below:
2. My solution:-
I have solved the first part of the question the one that I am having trouble solving is the second part. Here is my work on the solution.
For reference these are the variables that I have used in my solution:-
##\vec{s}_{s/e}=-(v_0\cos{\theta}t)\hat{i} + (v_0\sin{\theta}t-(1/2)gt^2)\hat{j}##
##\vec{s}_{b/e}=(v_0t)\hat{i}+(1-(1/2)gt^2)\hat{j}##
Now, to find the minimum distance between the bomb and the shell what I did was first find the relative displacement and then differentiate its modulus and set it as ##0## which gives us the minimum possible distance between them.
##\begin{aligned}
&\vec{s}_{s/b}=-(v_0\cos{\theta}+v_0)t\hat{i}+(v_0\sin\theta-1)\hat{j} \\
\implies & |\vec{s}_{s/b}|^2=2v_0^2t^2(1+\cos\theta)-2v_0\sin\theta t \qquad\qquad\qquad\qquad\qquad \ldots(1)
\end{aligned}##
Now, differentiating equation ##(1)## w.r.t ##t## and putting ##\dfrac{d|\vec{s}_{s/b}|^2}{dt}=0##, we get
##t=\dfrac{\sin\theta}{2v_0(1+\cos\theta)}=\dfrac{1}{4v_0}##
On substituting ##t=1/(4v_0)## in equation ##(1)##, we get
##{|\vec{s}_{s/b}|}^2=\dfrac{320}{16\times 25}=\dfrac{4}{5} \implies |\vec{s}_{s/b}|=\dfrac{2}{\sqrt5}##
3.Book's Solution:-
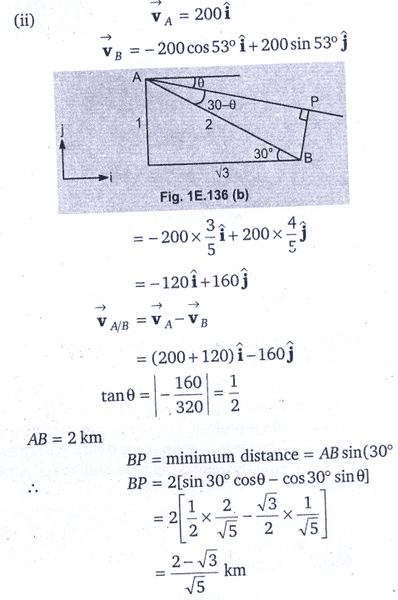
Why does my answer differ from the book, what did I miss.
An aircraft is flying horizontally with constant velocity = ##200 m/s##, at a height = ##1 km## above the ground. At the moment shown, a bomb is released from aircraft and the canon- gun below fires a shell with initial speed = ##200 m/s##, at some angle #\theta#.
1)For what value of ##'\theta'## will the projectile shell destroy the bomb in mid- air ? If the value of ##'\theta'## is ##53^{\circ}##.
2)Find the minimum distance between the bomb and the shell as they fly past each other. Take ##\sin53^{\circ}=4/5##.
The figure for the question is as shown below:
2. My solution:-
I have solved the first part of the question the one that I am having trouble solving is the second part. Here is my work on the solution.
For reference these are the variables that I have used in my solution:-
- ##\vec{s}_{s/e}##-Displacement of shell w.r.t Earth
- ##\vec{s}_{b/e}##-Displacement of bomb w.r.t Earth
- ##\vec{v}_{0}##-Velocity of bomb/shell w.r.t Earth
##\vec{s}_{s/e}=-(v_0\cos{\theta}t)\hat{i} + (v_0\sin{\theta}t-(1/2)gt^2)\hat{j}##
##\vec{s}_{b/e}=(v_0t)\hat{i}+(1-(1/2)gt^2)\hat{j}##
Now, to find the minimum distance between the bomb and the shell what I did was first find the relative displacement and then differentiate its modulus and set it as ##0## which gives us the minimum possible distance between them.
##\begin{aligned}
&\vec{s}_{s/b}=-(v_0\cos{\theta}+v_0)t\hat{i}+(v_0\sin\theta-1)\hat{j} \\
\implies & |\vec{s}_{s/b}|^2=2v_0^2t^2(1+\cos\theta)-2v_0\sin\theta t \qquad\qquad\qquad\qquad\qquad \ldots(1)
\end{aligned}##
Now, differentiating equation ##(1)## w.r.t ##t## and putting ##\dfrac{d|\vec{s}_{s/b}|^2}{dt}=0##, we get
##t=\dfrac{\sin\theta}{2v_0(1+\cos\theta)}=\dfrac{1}{4v_0}##
On substituting ##t=1/(4v_0)## in equation ##(1)##, we get
##{|\vec{s}_{s/b}|}^2=\dfrac{320}{16\times 25}=\dfrac{4}{5} \implies |\vec{s}_{s/b}|=\dfrac{2}{\sqrt5}##
3.Book's Solution:-
Why does my answer differ from the book, what did I miss.
Last edited: