surfhare75
- 3
- 0
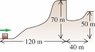
Here is the Problem. A 2.8-kg block slides over the smooth, icy hill shown in the figure .The top of the hill is horizontal and 70 m higher than its base. i attached the Figure Below.
What minimum speed must the block have at the base of the hill so that it will pass over the pit at the far side of the hill without falling into it?
I tried using .5mv1^2+m1gH=.5mv2^2+m2gH but I need to know the gap between the pit which is 40m. I believe I use H=.5gt^2 to find the time and use projectile motion x=vosin(x)t to find the distance.
What minimum speed must the block have at the base of the hill so that it will pass over the pit at the far side of the hill without falling into it?
I tried using .5mv1^2+m1gH=.5mv2^2+m2gH but I need to know the gap between the pit which is 40m. I believe I use H=.5gt^2 to find the time and use projectile motion x=vosin(x)t to find the distance.