kno
- 3
- 0
- Homework Statement
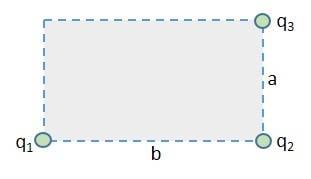
- Three point-like charges are placed at the corners of a rectangle as shown in the figure, a = 22.0 cm and b = 54.0 cm. Find the minimum amount of work required by an external force to move the charge q1 to infinity. Let q1= +3.00 µC, q2= −3.30 µC, q3= −3.60 µC.
- Relevant Equations
- W = -(EPE final - EPE initial)
W = -q * (V final - V initial)
This is the figure for the problem:
 1.) Solved for initial total EPE of the system
1.) Solved for initial total EPE of the system
EPE system = (kq2q3/a) + (kq2q1/b) + (kq1q3/√a^2 + b^2)
2.) Solved for final EPE of the system negating q1 as if it were off to infinity
EPE system final = (kq2q3/a)
3.) Plugged values into equation
W = -(EPE final - EPE intial)
I wasn't sure how to figure out the minimum work required, I think I am missing a step or two.
EPE system = (kq2q3/a) + (kq2q1/b) + (kq1q3/√a^2 + b^2)
2.) Solved for final EPE of the system negating q1 as if it were off to infinity
EPE system final = (kq2q3/a)
3.) Plugged values into equation
W = -(EPE final - EPE intial)
I wasn't sure how to figure out the minimum work required, I think I am missing a step or two.