amjad-sh
- 240
- 13
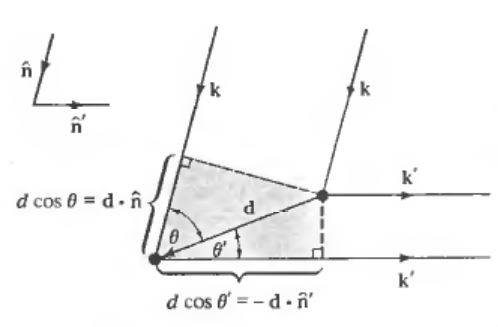
When we shine an X-ray beam on a crystal, according to Van Laue formulation, for a sharp intensity peak to be observed on the screen there is a specific direction ##\mathbf{\hat{n}}## , in which for all the X-rays with wavelength ##\lambda## and wavevector ##\mathbf{k}=\dfrac{2\pi}{\lambda}\mathbf{\hat{n}}## incident on the crystal, a scattered ray will be observed in a direction ##\mathbf{\hat{n}^{'}}## with wavelength ##\lambda## and wavevector ##\mathbf{k}^{'}=\dfrac{2\pi}{\lambda}\mathbf{\hat{n}^{'}}##. This must be occurred simultaneously for all the lattice points in the crystal and the path difference between the rays scattered by each of the lattice sites in the crystal must be an integral number of wavelength.
In other words, the condition that all scattered rays will interfere constructively is that:
$$\mathbf{R} \cdot(\mathbf{k}-\mathbf{k}^{'})=2\pi m$$
for integral ##m## and all Bravaise vectors ##\mathbf{R}##.
I have two questions related to this formulation:
(1) How all the wavevectors ##\mathbf{k}^{'}## can be scattered simultaneously from all the lattice points in the same direction ##\mathbf{\hat{n}}^{'}##? Is'nt the probability for such thing to happen very low?
(2) Von Laue assumed in his formulation that all the incident X-rays will hit the lattice points with the same wavevector ##\mathbf{k}##. But we know that the atomic separation in a crystalline solid is comparable in length to the wavelength of the X-ray. Therefore, when an X-ray comes across the first plane of lattice points, it will diffract, and I think hence that the X-ray incident on the second plane of lattice points would have a wavevector with magniude different from that incident on the first plane of lattice points. Is'nt this right? So why in the Von Laue formulation it is assumed that every incident X-ray hitting the lattice points has the same magnitude ##k##?
Thanks in advance :)
In other words, the condition that all scattered rays will interfere constructively is that:
$$\mathbf{R} \cdot(\mathbf{k}-\mathbf{k}^{'})=2\pi m$$
for integral ##m## and all Bravaise vectors ##\mathbf{R}##.
I have two questions related to this formulation:
(1) How all the wavevectors ##\mathbf{k}^{'}## can be scattered simultaneously from all the lattice points in the same direction ##\mathbf{\hat{n}}^{'}##? Is'nt the probability for such thing to happen very low?
(2) Von Laue assumed in his formulation that all the incident X-rays will hit the lattice points with the same wavevector ##\mathbf{k}##. But we know that the atomic separation in a crystalline solid is comparable in length to the wavelength of the X-ray. Therefore, when an X-ray comes across the first plane of lattice points, it will diffract, and I think hence that the X-ray incident on the second plane of lattice points would have a wavevector with magniude different from that incident on the first plane of lattice points. Is'nt this right? So why in the Von Laue formulation it is assumed that every incident X-ray hitting the lattice points has the same magnitude ##k##?
Thanks in advance :)
Last edited: