- #1
Livio Arshavin Leiva
- 29
- 9
I was reviewing an old topic for me that's x-ray diffraction, and one doubt I always had in my mind arised again.
When introducing the Bragg's law, the typical explanation is that the x-ray waves reflecting in two adjacent planes interfere with each other, leading to a fully constructive interference when the difference between the lengths of each wave's paths is a multiple of the wavelength, as it's shown in the image below from Wikipedia.
But in the case of this model being correct, one would had a maximum when the waves are coherent and zero intensity when the phase is 180°, but in between if one calculates the integral of the square of the resulting wave after interference it leads to a cosine law with the phase angle... so between two peaks of the same family (for example 100 and 200 Miller's indexes, that means that 1 and 2 wavelengths are exactly contained in the difference of path length, respectively) one should see a cosine dependence in the pattern (more or less, I know that the 2theta angle is not lineal with the phase between the waves (there's a sine relation)) but clearly the peaks of a real pattern are way sharper.
In fact, it's always said that according to theory, they should be deltas. But that's not Bragg's theory I guess, right?
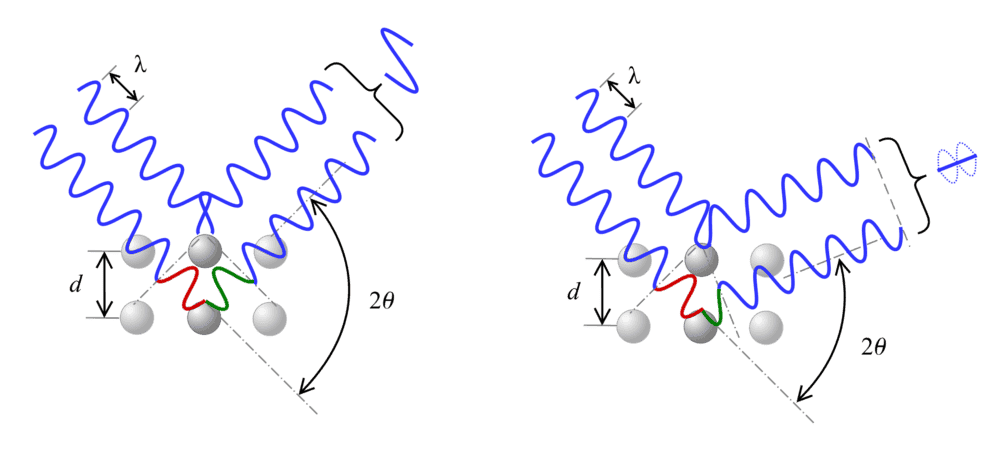
I know that this explanation is simplified and a more accurate (or more real) model is the von Laue's approach that considers spherical waves re-radiated by all atoms right after receiving the x-ray excitation wave. If one considers this, are the peaks sharper? I always heard that the two formulations were equivalent, but maybe they were equivalent only when looking at the constructive interference condition.
So my question is, to sum up, how can you explain that the peaks are so sharp?
Thank you in advance, and sorry if this is a noob question...
When introducing the Bragg's law, the typical explanation is that the x-ray waves reflecting in two adjacent planes interfere with each other, leading to a fully constructive interference when the difference between the lengths of each wave's paths is a multiple of the wavelength, as it's shown in the image below from Wikipedia.
But in the case of this model being correct, one would had a maximum when the waves are coherent and zero intensity when the phase is 180°, but in between if one calculates the integral of the square of the resulting wave after interference it leads to a cosine law with the phase angle... so between two peaks of the same family (for example 100 and 200 Miller's indexes, that means that 1 and 2 wavelengths are exactly contained in the difference of path length, respectively) one should see a cosine dependence in the pattern (more or less, I know that the 2theta angle is not lineal with the phase between the waves (there's a sine relation)) but clearly the peaks of a real pattern are way sharper.
In fact, it's always said that according to theory, they should be deltas. But that's not Bragg's theory I guess, right?
I know that this explanation is simplified and a more accurate (or more real) model is the von Laue's approach that considers spherical waves re-radiated by all atoms right after receiving the x-ray excitation wave. If one considers this, are the peaks sharper? I always heard that the two formulations were equivalent, but maybe they were equivalent only when looking at the constructive interference condition.
So my question is, to sum up, how can you explain that the peaks are so sharp?
Thank you in advance, and sorry if this is a noob question...
Last edited by a moderator: