Jdo300
- 548
- 5
Hello All,
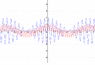
I have two questions regarding mixing of frequencies. I heard that there is a difference between two waves that simply ‘add’ mathematically, and two waves that are ‘multiplied’ mathematically. If I have two frequencies, say 10Hz and 11Hz and I add the waves together so that they produce a beat frequency. I attached a graph showing the difference between the two frequencies being summed and multiplied below. If this process were to occur inside an antenna. What kind of setups would be used to produce the two waveforms in the antenna?
My second question relates to resonant coupling. If the antenna were setup so that it produced the multiplied waveform, if there were an outside signal that was equal to the frequency of the beat wave in the antenna, would they couple to each other? (In this case, the outside wave would have a frequency of 1Hz). I know these frequencies are ridiculously low but just using them as examples to prove my point here (and match up with the graph I made). Any comments and suggestions welcome.
Thanks,
Jason O
P.S. NOTE: Blue graph is waves added and Red graph is waves multiplied.
I have two questions regarding mixing of frequencies. I heard that there is a difference between two waves that simply ‘add’ mathematically, and two waves that are ‘multiplied’ mathematically. If I have two frequencies, say 10Hz and 11Hz and I add the waves together so that they produce a beat frequency. I attached a graph showing the difference between the two frequencies being summed and multiplied below. If this process were to occur inside an antenna. What kind of setups would be used to produce the two waveforms in the antenna?
My second question relates to resonant coupling. If the antenna were setup so that it produced the multiplied waveform, if there were an outside signal that was equal to the frequency of the beat wave in the antenna, would they couple to each other? (In this case, the outside wave would have a frequency of 1Hz). I know these frequencies are ridiculously low but just using them as examples to prove my point here (and match up with the graph I made). Any comments and suggestions welcome.
Thanks,
Jason O
P.S. NOTE: Blue graph is waves added and Red graph is waves multiplied.