- #1
EEstudent90
Hi
I am trying to understand the figure 2 I have attached to this post.
From text:
Ok, I get that the air-gap flux density varies in a sinusoidal manner, because the air gap length is not constant i.e. non-constant reluctance and hence non-constant magnetic flux density.
What I do not understand is how we can draw the air gap MMF can be constant across the air gap?I am not very good in magnetics and Ampere's law etc., therefore my guess to why the MMF is constant across the air gap is by using Ampere's law with the red Ampere loop as shown in Figure 1.
Now my problem is that the MMF should change sign at B and D (according to attached Figure 2), right? How will Ampere's law handle this?
Again, not very good at this, hope someone can help me.Figure 1:
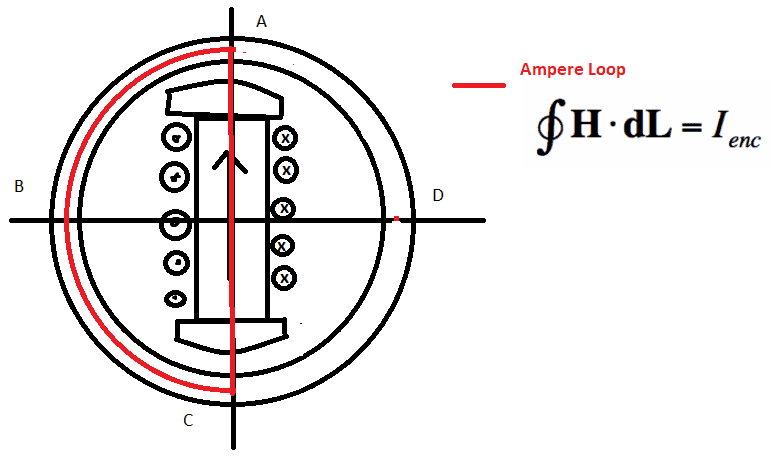
Figure 2:
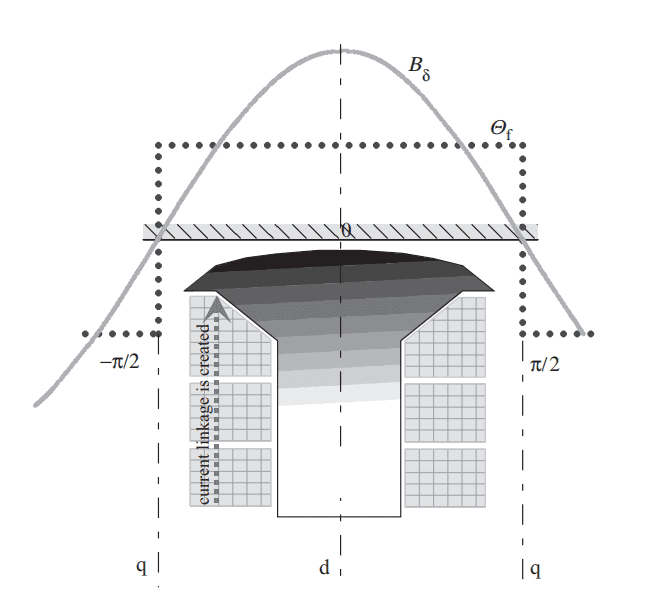
I am trying to understand the figure 2 I have attached to this post.
From text:
Due to the appropriate design of the pole shoe, the air-gap flux density varies cosinusoidally even though it is caused by the constant magnetic potential difference in the air gap.
Ok, I get that the air-gap flux density varies in a sinusoidal manner, because the air gap length is not constant i.e. non-constant reluctance and hence non-constant magnetic flux density.
What I do not understand is how we can draw the air gap MMF can be constant across the air gap?I am not very good in magnetics and Ampere's law etc., therefore my guess to why the MMF is constant across the air gap is by using Ampere's law with the red Ampere loop as shown in Figure 1.
Now my problem is that the MMF should change sign at B and D (according to attached Figure 2), right? How will Ampere's law handle this?
Again, not very good at this, hope someone can help me.Figure 1:
Figure 2: