Solve Modified Atwood Problem: Find T1, T2, T3, T4, T5 & F

  • Thread starter go2cnavy
  • Start date
  • Tags
    Atwood
In summary, the tension in a massless rope passing over two massless, frictionless pulleys is uniform throughout and is equal to the weight of the block (T1=mg). In addition, T2, T3, and T5 are all equal to each other, while T4 is equal but opposite to T3. The magnitude of the force F required to keep the system static is 0.8N and the total tension at T4 is equal to the sum of the pulley weights, T1, and F. In an example using a 200 gram hanging weight, T1=1.96N, T2=T3=49.98N, T4=149.94N, T5
  • #1
go2cnavy
19
0
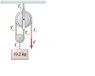
Q: A 10.2 Kg block is held in place by a massless rope passing over two massless, frictionless pulleys. Find the tensions T1, T2, T3, T4, T5 and the magitude of force F. Please see attached file for picture.

I know:

T1=mg=99.96N

My question, since the system is in equilibrium, shouldn't T2=T3=T5? IN addition, wouldn't T4 be equal but opposite to T3? I just get confused on how to set up the system of equations. Please help.
 

Attachments

  • quiz4.jpg
    quiz4.jpg
    12.6 KB · Views: 1,679
Physics news on Phys.org
  • #2
go2cnavy said:
My question, since the system is in equilibrium, shouldn't T2=T3=T5?
This is true because the rope is massless and the pulleys are frictionless, not because the system is in equilibrium. Under these conditions, the tension is uniform throughout that piece of rope.

IN addition, wouldn't T4 be equal but opposite to T3?
Why do you think that? Consider the top pulley: What forces pull up on it? What forces pull down?
 
  • #3
I had to see it for myself in a real world application. Today I set up the pulleys at physics lab and used a 200 gram mass as the hanging weight.

This gives my T1=mg=1.96 N.

The amount of force F required to keep the system static was .8N measured with a spring scale.

In addition, the pulley system was alos hanging from a spring scale and the tension at T4 was @ the sum of the pulley weights+T1+F.

If I let T1 = mg=(10.2)(-9.8)=-99.96N, Then is it safe to conclude that
T2+T3=99.96N so T2 and T3 each = 49.98N
 
  • #4
Sounds like you've got it. :approve:
 
  • #5
Thank you! I just found this site and will be here often now. Please check my work...

mg=99.98N
T1=99.96N
T2=49.98N
T3=49.98N
T4=-(mg+F)=149.94N
T5=49.98N
F=-49.98N
 
  • #6
Looks good. Two nitpicks: (1) Just give the magnitudes of the forces, forget the signs. (Tension in a rope is always positive.) (2) Round off to a reasonable number of significant figures. (Your results are not accurate to 4 digits!)
 
  • #7
Thank you for the help and the advice. Much appreciated!
 

1. What is the Modified Atwood Problem?

The Modified Atwood Problem is a physics problem that involves calculating the tension and forces on a system of masses connected by a pulley system. It is commonly used in introductory physics courses to test students' understanding of Newton's laws of motion and basic principles of mechanics.

2. What are T1, T2, T3, T4, T5, and F in the Modified Atwood Problem?

T1, T2, T3, T4, T5, and F are variables used to represent the tensions and forces in the pulley system. T1 and T2 are the tensions in the strings attached to the hanging masses, T3 is the tension in the string connecting the hanging masses, T4 and T5 are the tensions in the strings attached to the pulley, and F is the force of gravity acting on the masses.

3. How do you solve the Modified Atwood Problem?

To solve the Modified Atwood Problem, you first need to draw a free-body diagram of the system, labeling all the forces and tensions. Then, you can apply Newton's laws of motion and set up equations to solve for the unknown tensions and forces. Finally, you can use algebraic manipulation to solve for the values of T1, T2, T3, T4, T5, and F.

4. What are some common modifications to the Atwood Problem?

Some common modifications to the Atwood Problem include changing the masses of the hanging objects, adding more objects to the system, or changing the angle of the pulley. These modifications can make the problem more challenging and require different approaches to solve.

5. Why is the Modified Atwood Problem important in science?

The Modified Atwood Problem is important in science because it helps students understand fundamental concepts in mechanics, such as tension, forces, and Newton's laws. It also allows them to practice problem-solving skills and apply mathematical equations to real-life scenarios. Additionally, the Atwood Problem has practical applications in engineering and physics, making it a useful tool for understanding real-world systems.

Similar threads

How Do Tensions in a Massless, Frictionless Pulley System Compare?
    • Introductory Physics Homework Help
Replies
1
Views
2K
Solving Otto Cycle Problem: Find p2, p3, p4, T2, T3, T4, V2, V3, V4
    • Introductory Physics Homework Help
Replies
1
Views
3K
Find the acceleration of the hanging block
    • Introductory Physics Homework Help
2
Replies
64
Views
12K
Blocks, Pulley, Ropes, and Tension
    • Introductory Physics Homework Help
Replies
10
Views
6K
Rotational Dynamics Pulley Problem Help needed
    • Introductory Physics Homework Help
Replies
4
Views
2K
Multi-pulley and force problem
    • Introductory Physics Homework Help
Replies
2
Views
4K
Simple Pulley Ratios: Find T1, T2, T3, T4, T5, F
    • Introductory Physics Homework Help
Replies
15
Views
13K
Suspended Block: Find Tensions T1 & T2
    • Introductory Physics Homework Help
Replies
2
Views
2K
Solving Pulley System Questions: Tensions, Weights, and F=ma
    • Introductory Physics Homework Help
Replies
1
Views
3K
2 blocks connected by massless string VS. pulley system
    • Introductory Physics Homework Help
Replies
4
Views
2K

Hot Threads

Recent Insights

Back
Top