- #1
Konte
- 90
- 1
Hello everybody,
I am new in this forum and also new with english langage, so don't be shocking if I write like a baby for you. I am little better for understanding when I read.
My question:
Books always tell us about the only ground state of ammonia molecule but never on its excited state. So, I am thinking to myself, could we try to study the first excited state of this molecule by copying the method used for the ground state?
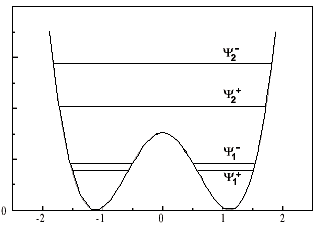
I mean: for the ground state, there is a pair of eigenstate designed by [itex]\psi_1^+[/itex] and [itex]\psi_1^-[/itex] whith which we can construct another pair of orthogonal state designed by [itex]\phi_1^L[/itex] and [itex]\phi_1^R[/itex]. With those basis, the dynamic of the ground state of the molecule is understood.
My question is about generalizing this approach on the other pair of excited level. From the second pair of eigenstate [itex]\psi_2^+[/itex] and [itex]\psi_2^-[/itex], could we construct a kind of [itex]\phi_2^L[/itex] and [itex]\phi_2^R[/itex] ?
Thank you everybody.
I am new in this forum and also new with english langage, so don't be shocking if I write like a baby for you. I am little better for understanding when I read.
My question:
Books always tell us about the only ground state of ammonia molecule but never on its excited state. So, I am thinking to myself, could we try to study the first excited state of this molecule by copying the method used for the ground state?
I mean: for the ground state, there is a pair of eigenstate designed by [itex]\psi_1^+[/itex] and [itex]\psi_1^-[/itex] whith which we can construct another pair of orthogonal state designed by [itex]\phi_1^L[/itex] and [itex]\phi_1^R[/itex]. With those basis, the dynamic of the ground state of the molecule is understood.
My question is about generalizing this approach on the other pair of excited level. From the second pair of eigenstate [itex]\psi_2^+[/itex] and [itex]\psi_2^-[/itex], could we construct a kind of [itex]\phi_2^L[/itex] and [itex]\phi_2^R[/itex] ?
Thank you everybody.
 I too would recommend the Bunker & Jensen book. There are a lot of things with spectroscopy that are historical, that tend to obfuscate, and this book does a very good job of clearing away the cobwebs and showing the molecular physics in modern terms, without the barouque curlicues decorating everything.
I too would recommend the Bunker & Jensen book. There are a lot of things with spectroscopy that are historical, that tend to obfuscate, and this book does a very good job of clearing away the cobwebs and showing the molecular physics in modern terms, without the barouque curlicues decorating everything.