adjacent
Gold Member
- 1,552
- 62
Homework Statement
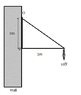
Find the other forces present.
Assume the triangle to be weightless
Homework Equations
τ=Force x perpendicular distance
The Attempt at a Solution
The force,10N provides a 50Nm Torque. (10 x 5)
The triangle is in equilibrium so,anticlockwise moment is equal to clockwise moment
50Nm=2 x F
F=25N at p
But within the two meters,not only p touches but other parts of the triangle(in contact with the wall) touches too.
Should I account for that?
As the net force should be zero,pivot point exerts a force of 25N to the left.and 10N upwards.
Is this correct?
Attachments
Last edited: