masterchiefo
- 211
- 2
Homework Statement
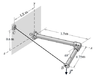
An OAB pipe is embedded in O. A cable BC = 1000N and F = ( 0,-f , 0) act on B.
Question:
Determine the magnitude of the force F as the resultant moment about the axis OA is canceled.
Picture in attachment:
Homework Equations
The Attempt at a Solution
O=(0 0 0)
A=(1.5 0 0)
B=(1.5 -sin(40)*0.75 cos(40)*0.75)
C=(0 0.6 1.2)
VTBC= 1000*unit(C-B)
VF=(0 -f 0)
VO=(0 Oy Oz) ==translation forces at o
vMo=(0 momenty momentz) == rotational forces at o
translation equilibrium = VO + VTBC + VF = (0 0 0)
VFxrOB*uAO => crossP(b-o,vf)*unitV(a-o)= (0 0 0)
crossp function = cross product of two vectors.
unitV function = unit vector
F = ??
Calculating moment from an axis is confusing me a lot.
I thank you in advance for helping me.
Attachments
Last edited: