Moment(torque) help (bycicle crankset)

[KansaiRobot]

Hello everybody.
I would appreciate your help in something I have been thinking all day (and now I am doing an allnighter, without result ) (by the way, this is not "homework" since I am not at school. I have written the questions as well)

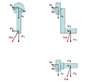
Please take a look at the attached pic. It is a bycicle crankset. Now

1) There is a sensor in the center. It can sense Fx, Fy and Fz and also Mx, My and Mz. (where F are forces and M moments (or torques))

2) The rider applies a Total force (Ftot) in the pedal. This Total Force can be decomposed as (F"x, F"y, F"z)-> just a notation.

My problem is that I have to find Ftot and the only data I have is the force and moments in the sensor.
----------------------------------

Now, I have done this so far:

1) I can see that Mz and Mx　are generated ONLY by F"y. So I guess I can find F"y quite easily:

||F"y||= ||Mz||/(radius of crank)


2) I can see that Mｙ is generated by BOTH F"x and F"z.

----------------------

Now how can I get F"x and F"z from My (data)?


On related notes what is the relationship between the forces at the pedal(F"x, F"y, F"z) and the forces at the sensor? (Fx, Fy, Fz)
THIS is KEY I think!

Any help would be greatly appreciated

Thanks
Kansai

 

[jack action]

If the forces involved are all in the diagrams you've shown, the forces are equal and opposite in each direction and:

(Ftot)² = (Fx)² + (Fy)² + (Fz)²

 

[KansaiRobot]

Thanks for the reply.

I don't know if I have been misleading with my not-so-good graphics.

The user applies a force (Ftot) over the pedal.

when I draw Fx, Fy and Fz (on the sensor) what I meant was that the sensor senses forces there. I didnt mean that there are aditional forces applied there. i don't know if I made sense, sorry.

I am thinking that somehow Fx and Fz (forces "sensed" at the sensor) are proportional to F"x and F"z(real forces applied to the pedal)

Any thoughts please?