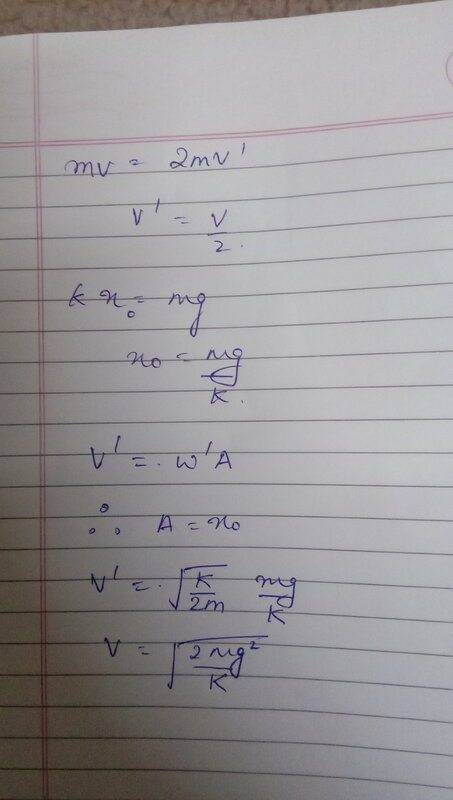Prabs3257
- 65
- 4
- Homework Statement
- A block A of mass m is in equilibrium after being suspended from the ceiling with the help of a spring of force constant k. The block B of mass m strikes the block A with a speed v and sticks to it.The value of v for which the spring just attains its natural length is
- Relevant Equations
- Momentum conservation
I first got the velocity of the combined mass with conservation of momentum and as it was in the mean position the velocity can be written as v = wA ( w= angular frequency , A = amplitude ) as we have to take it back to natural length i put A as the initial extension but i am getting a wrong ans can someone please tell me what i did wrong . Please refer to my work in the attachment below