Jus10
- 12
- 2
This is a continuation of a previous thread in which I was informed my TA was mistaken on an aspect of magnetism. This thread is just to verify another problem within the homework is correct. Other threads will be posted to continue.
1. Homework Statement
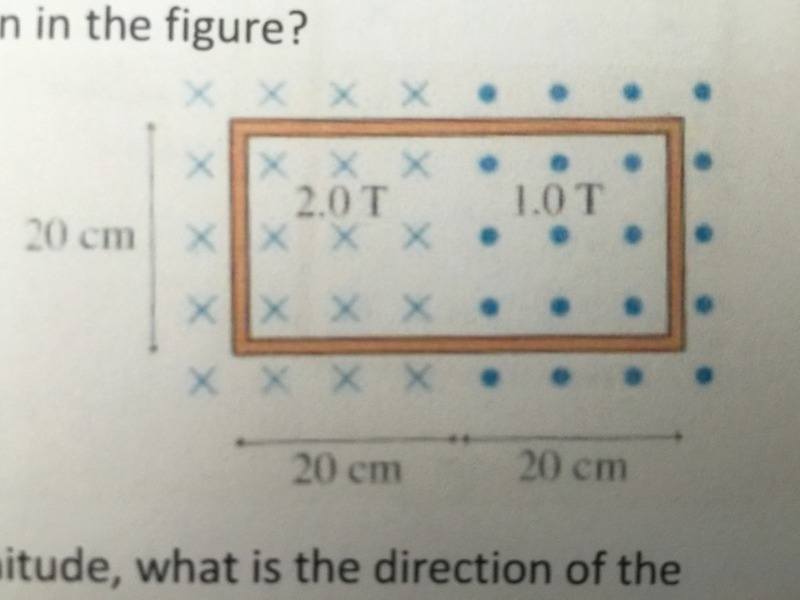
A) What is the magnetic flux through the loop shown in the figure.
B) If both magnetic fields begin to decrease in magnitude, what is the direction of the induced current in the loop? Explain with Lenz's Law.
Φ = BA
Part A) Φ = (BinAin)-(BoutAout)
Φ = (2.0)(0.22)-(1.0)(0.22)
Φ = 0.04 Wb
Part B) The induced field would act in the direction of the applied field if B is decreasing. Therefore, the current would be flowing clockwise.
1. Homework Statement
A) What is the magnetic flux through the loop shown in the figure.
B) If both magnetic fields begin to decrease in magnitude, what is the direction of the induced current in the loop? Explain with Lenz's Law.
Homework Equations
Φ = BA
The Attempt at a Solution
Part A) Φ = (BinAin)-(BoutAout)
Φ = (2.0)(0.22)-(1.0)(0.22)
Φ = 0.04 Wb
Part B) The induced field would act in the direction of the applied field if B is decreasing. Therefore, the current would be flowing clockwise.