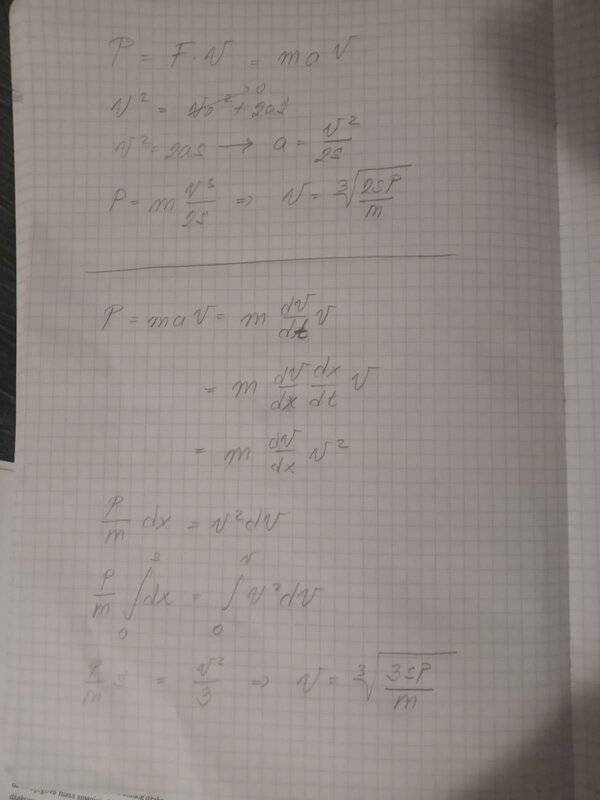Motion equation problem -- Car accelerating with a constant power engine

[Weber_per_metermeter]

Homework Statement

In horizontal straight line path, there's a car, weighing 600kg, fully powered with P=25kW, that is constant during motion. Car is starting from rest state (v0=0). What is the speed intensity after s=125m of driving? Enviromental resistance and friction are negligible.

Relevant Equations

P=F*v=m*a*v
v^2=v0^2+2as

So I tried to solve this in two methods, but I keep getting different results, and I don't know why.

 

[haruspex]

It's hard to read, but you seem to be using SUVAT equations. Those only apply when acceleration is constant. Here, power is constant.
Write the differential equation that expresses that.

Edit: managed to get a clearer image of your work, and I see you did use the right method in the second attempt, as @TSny notes.

 

[TSny]

Your first method is not correct due to the reasons @haruspex mentioned. Your second method looks OK to me.

 

[Weber_per_metermeter]

Thank you for your answer. Now that you mentioned it, of course its due to non constant acceleration :D
Great work!