Whatazarian
- 3
- 0
[SOLVED] Motion in one dimension
To protect his food from hungry bears, a boy scout raises his food pack with a rope that is thrown over a tree limb at height h above his hands. He walks away from the vertical rope with constant velocity V^{1}_{boy}, holding the free end of the rope with his hand.
(a) Show that the speed V of the food pack is given by x(x^{2}+h^{2})^{-1/2}V^{1}_{boy} where x is the distance he has walked away from the vertical rope.
(b) Show that the acceleration a of the food pack is h^{2}(x^{2}+h^{2})^{-3/2}V^{2}_{boy}.
h^{2}(x^{2}+h^{2})^{-3/2}V^{2}_{boy}=a
x(x^{2}+h^{2})^{-1/2}V^{1}_{boy}=V
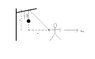
First of all I would advise you all to look at the attached diagram of the situation (as expressed in the question).
First, I concluded that V^{1}_{boy}= x/t, since the boy travels a distance of x in some time t. Then, knowing that the boy started at x = 0, I calculated the distance the pack covered in this time would be (x^{2}+h^{2})^{1/2} by Pythagoras' Theorem. Hence, V= ((x^{2}+h^{2})^{1/2})/t, and since t =x/V^{1}_{boy} we can conclude that V = V^{1}_{boy}((x^{2}+h^{2})^{1/2})/x by substitution.
Am I right or wrong? Obviously if you switch the distances around, the equation would come out as expected, but, I cannot fathom why and how they would be the other way around.
b) Taking V from a), and dividing by t to give acceleration, a = V^{2}_{boy}((x^{2}+h^{2})^{1/2})/x^{2}
or a = (V^{2}_{boy}x)/((x^{2}+h^{2}))
From there I don't know what to do since the acceleration is changing, so my method is probably wrong.
Any help would be appreciated.
Homework Statement
To protect his food from hungry bears, a boy scout raises his food pack with a rope that is thrown over a tree limb at height h above his hands. He walks away from the vertical rope with constant velocity V^{1}_{boy}, holding the free end of the rope with his hand.
(a) Show that the speed V of the food pack is given by x(x^{2}+h^{2})^{-1/2}V^{1}_{boy} where x is the distance he has walked away from the vertical rope.
(b) Show that the acceleration a of the food pack is h^{2}(x^{2}+h^{2})^{-3/2}V^{2}_{boy}.
Homework Equations
h^{2}(x^{2}+h^{2})^{-3/2}V^{2}_{boy}=a
x(x^{2}+h^{2})^{-1/2}V^{1}_{boy}=V
The Attempt at a Solution
First of all I would advise you all to look at the attached diagram of the situation (as expressed in the question).
First, I concluded that V^{1}_{boy}= x/t, since the boy travels a distance of x in some time t. Then, knowing that the boy started at x = 0, I calculated the distance the pack covered in this time would be (x^{2}+h^{2})^{1/2} by Pythagoras' Theorem. Hence, V= ((x^{2}+h^{2})^{1/2})/t, and since t =x/V^{1}_{boy} we can conclude that V = V^{1}_{boy}((x^{2}+h^{2})^{1/2})/x by substitution.
Am I right or wrong? Obviously if you switch the distances around, the equation would come out as expected, but, I cannot fathom why and how they would be the other way around.
b) Taking V from a), and dividing by t to give acceleration, a = V^{2}_{boy}((x^{2}+h^{2})^{1/2})/x^{2}
or a = (V^{2}_{boy}x)/((x^{2}+h^{2}))
From there I don't know what to do since the acceleration is changing, so my method is probably wrong.
Any help would be appreciated.
Last edited: