Motion of a particle in a rotating tube

[AwesomeTrains]

Homework Statement

Hello everyone,
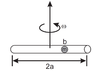
How do I go about this problem; Describe the motion of the particle, m, inside the rotating tube. (See attachment please.)
At time t=0, r(t=0)=b and \dot{r}(t=0)=v_{0}

Homework Equations

I think it would be practical to use polar coordinates to describe the system.
Then maybe find the kinetic energy and the potential, to find the Lagrangian?

The Attempt at a Solution

I don't really know where to start, any hints or tips are really appreciated.
In class we just started with holonomic constraints, therefore I'm a little new to this concept. I guess it has something to do with this problem?

 

[Simon Bridge]

I think it would be practical to use polar coordinates to describe the system.
Then maybe find the kinetic energy and the potential, to find the Lagrangian?

That would work - you could also change to a coordinate system that rotates with the tube.
What has your coursework concentrated on just lately?

 

[AwesomeTrains]

Yea, in the problem statement they also hint that it can be viewed as a one dimensional motion in a coordinate system rotating with the tube. How would I go about that?
At the moment we are doing this: http://en.wikipedia.org/wiki/Holonomic_constraints and we derived the euler lagrang equation. But I am not sure how to use it. Can you give me a hint of what to do next?

 

[BiGyElLoWhAt]

Are there any forces acting on the particle other than the centripetal force?

 

[Orodruin]

Why don't you try doing exactly what you suggested (express the kinetic and potential energies to find the lagrangian) and then tell us what you get?

To get you started,a sk yourself: what is the kinetic energy? And what are the constraints?

 

[AwesomeTrains]

Thanks for the help. I have found another method of solving the problem, which I find more simple. Posting it if anyone should be interested.

\vec{F}=m\ddot{\vec{r}} and because the only force acting on the particle is the centrifugal force (Conditions give that there is no friction and gravity): \vec{F}=-m\vec{\omega}\times(\vec{\omega}\times\vec{r})
In a plane this reduces to: \ddot{\vec{r}}=-\omega^{2}r
Which can be solved with an exponential function I believe. (Omega and two start conditions were given.)

(Lagrange will be on the next problem sheet

 

[Simon Bridge]

... with the note that you are implicitly using a rotating reference frame whenever you invoke "centrifugal force".

 

[Orodruin]

And to be quite honest, the Lagrange approach is just as easy (if not easier) in this case. There is no potential energy term so the only thing you need to give an expression for is the kinetic energy
$$
T = \frac{m}{2} (\dot x^2 + \dot y^2).
$$
Insert the constraint conditions $x = r \cos(\omega t)$ and $y = r \sin(\omega t)$ into $T$, apply the EL equations, and you arrive at $\ddot r = \omega^2 r$ without referencing fictitious forces.

In a plane this reduces to: \ddot{\vec{r}}=-\omega^{2}r

Note that the equation you have given here has two problems: (1) the LHS is a vector and the RHS is a scalar. (2) The acceleration should be parallel and not anti-parallel to the displacement.

 

[AwesomeTrains]

Thanks for correcting me and for the help :)
This week we got two new problems where you have to use Lagrange.