How Does Motional EMF Affect Electron Distribution in a Conductor?

[Gerry Rzeppa]

Here is a typical description of motional EMF:

"The figure below shows a conducting rod of length L being moved with a velocity v in a uniform magnetic field B:

The magnetic force acting on a free electron in the rod will be directed upwards. As a result, electrons will start to accumulate at the top of the rod. The charge distribution of the rod will therefore change, and the top of the rod will have an excess of electrons (negative charge) while the bottom of the rod will have a deficit of electrons (positive charge). This will result in a potential difference between the ends of the rod equal to LvB."

My question is: How do we calculate the number of excess/deficit electrons for a given L, v, and B?

 

[mfb]

Calculate the voltage that leads to a force equilibrium, and then the corresponding charge densities (the second part can be messy in the general case).

 

[Gerry Rzeppa]

I'm going to need a little more help with the math (it's a weakness of mine).

Calculate the voltage that leads to a force equilibrium...

That sounds like LvB to me. Yes? If so, let's say we select L and v and B so LvB is 1 volt.

...and then the corresponding charge densities (the second part can be messy in the general case).

And I'm stuck.

 

[mfb]

There are methods to calculate a charge distribution for a given field distribution. But if you want to do that properly, then you have to consider that your conductor has a finite size, and do those calculations in three dimensions.

Where do you plan to use the charge distribution?
If you are just interested in an order of magnitude, assume your rod is a capacitor with large plates (large compared to the gap size), and calculate the charge density there.

 

[Jeff Rosenbury]

It is a complicated problem. You need to know what the charge distribution is in your particular alloy (charge carriers/unit volume). In most materials electrons dominate, but not always.

In addition, once the charges start to move, eddy currents will form. That's not a problem if something is pushing the rod at a constant speed; the push will just push harder. But in the real world there might be slowing due to power loss in the eddy currents, etc.

 

[Gerry Rzeppa]

It is a complicated problem...

Rats! I was hoping for something simple like the definition of current: "1 amp is equal to 6.28x10^18 electrons moving past a point every second." Or perhaps a simple equation like E=LvB or F=ma or E=IR.

Where do you plan to use the charge distribution? If you are just interested in an order of magnitude...

The ultimate goal is to explain the workings of a basic vacuum tube guitar amp circuit to a ten-year-old in electron-flow terms. Electron-flow terms because the workings of vacuum tubes are invariably described from an electron-flow perspective. (I realize this is an unusual approach to circuit analysis in these modern times, but it seems appropriate to me in this particular case.) Consider, for example, this excerpt from a book explaining how the varying flow of electrons coming out of a vacuum tube is converted to changes in voltage that are passed on to the next stage of the amp:

I think that's something the kid can easily picture: the varying voltage (at the point marked with the blue arrow) is the result of the varying excess/deficit of electrons at that spot (relative to ground). Which reminded me of descriptions of motional EMF from my college days (decades ago): hence this thread. After all, I thought, we're able to define current easily enough in terms of electron flow; perhaps we can similarly define voltage for the kid in terms of electron concentration (eg, excess electrons per proton, or per cubic centimeter, or something like that) and he can thus picture voltage (not as some abstract quantity with units of measure he's never heard of -- like "joules" and "coulombs" -- but) as the natural result of the mutual repulsion of electrons; as a measure of the electron's "unhappiness" or "dissatisfaction" at being unnaturally crammed together; a measure of their desire to redistribute themselves.

 

[Jeff Rosenbury]

That sounds like a fair description. The electron flow model has some serious weaknesses, but as long as you understand that, it's a good intuitive model.

The reason the problem is hard is not conceptual. It's hard because it's hard to know how many free electrons are in a wire. It's hard to know how they self interact. These difficulties are more in measurement than concept.

 

[Gerry Rzeppa]

That sounds like a fair description. The electron flow model has some serious weaknesses, but as long as you understand that, it's a good intuitive model. The reason the problem is hard is not conceptual. It's hard because it's hard to know how many free electrons are in a wire. It's hard to know how they self interact. These difficulties are more in measurement than concept.

Well, how about just an order-of-magnitude kind of guess for me? If one amp is a gazillion electrons (6.28x10^18) moving past a point per second, roughly how many "excess" or "displaced" or "accumulated" electrons does it take to get, say, a 1-volt peak out of that vacuum tube?

 

[mfb]

You cannot convert voltage to electron density, that does not work. They are completely different things.
For a specific setup they can be proportional to each other, but then the factor between them depends on the setup. As analogy: there is no fixed time you need to travel 100 kilometers. For a given transportation mode (walking, car on a highway, airplane, light...) you can make a good guess how long it will take, but a general relation does not exist, not even as order of magnitude.

 

[Jeff Rosenbury]

You cannot convert voltage to electron density, that does not work. They are completely different things.
For a specific setup they can be proportional to each other, but then the factor between them depends on the setup. As analogy: there is no fixed time you need to travel 100 kilometers. For a given transportation mode (walking, car on a highway, airplane, light...) you can make a good guess how long it will take, but a general relation does not exist, not even as order of magnitude.

I disagree. One can convert electron density to voltage. It is called capacitance. There are other factors involved such as geometry, but a capacitor does just that.

A 1 Farad capacitor contains 1 Coulomb of electrons.

So to answer the OP's question, it depends on the capacitance of the tube element (the grid?). Conveniently 1 Coulomb per second is an Amp. So that gives you an order of magnitude.

You might want to study what affects the capacitance to understand more about how charge turns into voltage.

 

[mfb]

I disagree. One can convert electron density to voltage. It is called capacitance. There are other factors involved such as geometry, but a capacitor does just that.

Capacitance depends on the setup, that's my point.
Also, charge and charge density are not the same thing either.

 

[Gerry Rzeppa]

1. It seems to me that these two devices are conceptually similar:

The air molecules on the left are analogous to the electrons on the right, and the upward force of the piston is analogous to the upward force of the magnetic field. The air molecules like it less and less as they are pressed closer and closer together, and will immediately separate and distribute themselves more evenly given the opportunity; ditto for the electrons. It seems to me that we ought to be able to somehow relate electrons per cubic inch (or per proton, or something) to voltage (electrical pressure) in the same way that we intuitively relate "molecules per cubic inch" to air pressure.

2. Regarding capacitance: I'm sorry, but I don't see how capacitance applies in this case. The rod is conductive through and through -- it has no insulating dielectric that is being stretched or deformed due to the difference in electron concentration at the ends, and so it just doesn't look like a capacitor to me.

3. It seems odd to me that we can't get a relationship between voltage and a specific number of electrons even though we know that E=IR and that I is defined as 6.28x10^18 electrons per second past a given point. I don't understand the units of measure well enough, and my math isn't good enough, to get me further, but it seems like we ought to be able to relate the two based on that formula and that definition of current.

4. Thought experiment: Let's select L and v and B in the above drawing so LvB equals 1 volt. Then, while the rod is moving, let's connect a 1-ohm resistor across the ends of it. When we do (assuming we keep moving the rod at velocity v) we'll be pushing 1 amp's worth of electrons past any given point in the circuit every second: 6.28x10^18, to be specific. Now, without stopping the rod, we disconnect the resistor. The electrons will continue to "flow" upward until -- until what? Until, I would think, the force exerted by the mutual repulsion of the accumulated electrons at the top of the rod equals the upward force of the field. My guess is that this would be 1 amp's worth (or 6.28x10^18) since this is the number we were able to move, continuously, when we had a 1-ohm path all the way around. But of course that's just an intuitive guess from someone who is more of an artist than a mathematician. What would you guys estimate?

 

[mfb]

Even if we fully simulate the problem, the result cannot be a single number of electrons. You will get a large charge density at the top, gradually decreasing as you go down, crossing zero somewhere in the middle, increasing (but with opposite charge) again until you reach the bottom. That is not a number, that is a distribution - and, as mentioned, it is not easy to calculate it.

You'll certainly not move 1 C of charges around. That would be a ridiculously huge amount of charge separation. And there is no reason to expect anything special about that arbitrary, man-made definition of a unit.

 

[Jeff Rosenbury]

Gauss's Law relates charge density to voltage. It states that the electric field over a closed surface is equal to the charge enclosed by that surface.

∫ E ⋅ ds = (1/ε_º) ∫ ρ dv

Notice this equation depends on geometry as well as the permittivity.

Your question seemed to be about a tube. Why is that not like a capacitor? There are conductors separated by a dielectric (vacuum).

As for the rod, I seem to recall mentioning eddy currents. You are the one putting charges on the ends due to your analogy. I tend to think much the same way, but I recognize it's just an analogy. The electrons don't pile up at the ends because it's a conductor and they move around in the magnetic field.

 

[Gerry Rzeppa]

Even if we fully simulate the problem, the result cannot be a single number of electrons. You will get a large charge density at the top, gradually decreasing as you go down, crossing zero somewhere in the middle, increasing (but with opposite charge) again until you reach the bottom. That is not a number, that is a distribution - and, as mentioned, it is not easy to calculate it. You'll certainly not move 1 C of charges around. That would be a ridiculously huge amount of charge separation.

As for the rod, I seem to recall mentioning eddy currents. You are the one putting charges on the ends due to your analogy. I tend to think much the same way, but I recognize it's just an analogy. The electrons don't pile up at the ends because it's a conductor and they move around in the magnetic field.

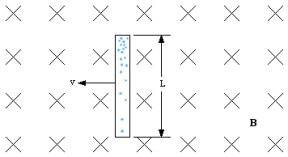
I understand that it's nearly impossible to track individual electrons (as my earlier drawings might have suggested). So let's use these drawings, where I've added conductive rails for the rod to ride on, and where the concentration of electrons is represented as a gradient, darker blue meaning more electrons in that area:

Now assume that L and v and B have been chosen so LvB is 1 volt, and that the rod is moving steadily to the right.

1. If the overall resistance of the left loop is 1 ohm, then by Ohm's Law (I=E/R) the flow of free electrons must be 1 amp's worth and the concentration of free electrons equal throughout the circuit (as indicated by the uniform blue color). Which means 6.28x10^18 electrons must be moving past any point in that circuit every second. Yes?

2. Now let's increase the resistance of the loop to say, 2 ohms, as depicted in the drawing in the center. Since LvB is still 1 volt, Ohm's Law now gives us 1/2 amp of flow or 3.14x10^18 electrons per second past any point in the circuit. But it seems to me there's still a potential (no pun intended) for greater flow since L and v and B haven't changed. In other words, there will be an excess of electrons at the top and a corresponding deficit of electrons at the bottom of the circuit in this case I've indicated this with the revised gradient -- darker than the center drawing at the top, and lighter at the bottom. Yes?

3. Finally, let's make the resistance of the loop ridiculously large by opening the circuit as in the drawing on the right. Current, in this case, will be negligible. But the potential (LvB) will still be 1 volt. Which means, according to the description of motional EMF at the very top of this thread, that the number of excess electrons at the top (and the corresponding deficit of electrons at the bottom) will be the maximum for this configuration and the selected L, v, and B variables. We thus get very dark blue at the top and a correspondingly very light blue at the bottom. Yes?

So (assuming all that is corrent) we know both the flow (6.28x10^18 electrons per second past any spot) and the relative concentration (equal everywhere) in the left case. And we know the flow (3.14x10^18 electrons per second past any spot) in the center case, and the flow (zero) in the right case. What we don't know is the relative (or absolute) concentration of electrons in the latter two cases.

It seems to me we ought to be able to calculate at least the relative concentrations in these latter cases by drawing a horizontal line through the middle of the circuit and averaging what's above and what's below.

And it seems to me that we ought to be able to calculate absolute concentrations once we figure out what to put in the denominator of those figures (ie, per proton, or per cubic centimeter, or something like that). After all, the energy is stored by pressing the electrons closer together than they want to be, which strikes me like compressing a spring (and where the stored potential energy is a simple 1/2kx^2).

Gauss's Law relates charge density to voltage. It states that the electric field over a closed surface is equal to the charge enclosed by that surface. ∫ E ⋅ ds = (1/ε_º) ∫ ρ dv Notice this equation depends on geometry as well as the permittivity.

Too bad calculus is out of the reach of my ten-year-old. And me (since I haven't used it much since I graduated from college decades ago).

Your question seemed to be about a tube. Why is that not like a capacitor? There are conductors separated by a dielectric (vacuum).

Yes, but I wasn't asking about the relative concentration of electrons on the plate versus the cathode. I was asking about the relative concentration of electrons at a point in the circuit where only resistive elements are involved. We get the same kind of "pile up" of electrons at the pickup end of the guitar amp where no tubes are involved:

As you can see, I've attempted to illustrate the relatively high-voltage (2-volt) / low current (it's nanoamps) behavior of the circuit using the same kind of picture we get with motivational EMF above. Specificially, (a) uniform current throughout the circuit (the darker blue electrons), but (b) not uniform concentration of electrons (dark and light together). It is my understanding that it is this varying concentration of electrons that gives us the voltage swing, both here and in that junction between plate and plate resistor discussed earlier.

What bothers me is that I can tell the kid exactly how many electrons are flowing in that circuit at any point in time (since the current is known), but I can't tell him even what ratio of electrons it takes to account for those varying voltages. Seems like I ought to be able to do that without the need for higher mathematics.

 

[mfb]

and the concentration of free electrons equal throughout the circuit

The concentration won't be the same everywhere.
There is no fundamental difference between the 1 Ohm and 2 Ohm case here. In both cases the electron density will be non-uniform.

There is nothing special about "1 [Unit]" in general. We could have completely different unit systems, and physics would not change at all. We could have defined 1 Ampere as 1 electron per second, or 1 electron per year. Would you expect 1 electron separation (in some way) then?

3. Finally, let's make the resistance of the loop ridiculously large by opening the circuit as in the drawing on the right. Current, in this case, will be negligible. But the potential (LvB) will still be 1 volt. Which means, according to the description of motional EMF at the very top of this thread, that the number of excess electrons at the top (and the corresponding deficit of electrons at the bottom) will be the maximum for this configuration and the selected L, v, and B variables. We thus get very dark blue at the top and a correspondingly very light blue at the bottom. Yes?

Right. But we don't get the amount from that consideration. Also, "very large" is probably of the order of pico- to nanocoulombs for typical lab setups.

 

[Gerry Rzeppa]

But we don't get the amount [of EMF?] from that consideration. Also, "very large" is probably of the order of pico- to nanocoulombs for typical lab setups.

It sounds like you want to re-word the description of motional EMF at the top of this thread to read (implied changes in bold):

"The magnetic force acting on a free electron in the rod will be directed upwards. As a result, an insignificant number of electrons will start to accumulate at the top of the rod. The charge distribution of the rod will therefore change, but not in any significant way, and the top of the rod will have an insignificant excess of electrons (negative charge) while the bottom of the rod will have an insignificant deficit of electrons (positive charge). This excess/deficit of electrons will not result in a potential difference between the ends of the rod equal to LvB, though the potential difference will be equal to LvB due to other unspecified considerations."

At least that's what I'm hearing.
​

 

[Jeff Rosenbury]

The relationship between voltage and charge carriers is the capacitance. The fact that something doesn't look like a capacitor has nothing to do with it.

Capacitance exists nearly everywhere, even in solid copper. The only requirement is a separation of charges. Most circuits have stray capacitance which engineers work on reducing for high frequency work. It's why component sizes keep getting smaller as computers get faster.

In your diagrams, there is an electric field (voltage) between the horizontal bars. There is a capacitance as well. To know how many electrons are there, find the capacitance. One Farad equals one Coulomb per Volt. It is a simple equation. Most capacitors are well under 1 F. Stray capacitance is usually in the nF or pF range. Tubes are likely on the high end of that.

As an example, here's the datasheet for the popular 12AX7 tube. It lists all the inter-electrode capacitances.

 

[Gerry Rzeppa]

In your diagrams, there is an electric field (voltage) between the horizontal bars. There is a capacitance as well. To know how many electrons are there, find the capacitance. One Farad equals one Coulomb per Volt.

Again, it seems to me that the capacitance of the three devices below is not pertinent: none of them is able to store any significant potential when the rod is not moving -- the electrons too quickly redistribute themselves evenly -- so none of them behaves like a capacitor.

But let's say you're right: how do I find the capacitance in these three cases? (Six if we count "rod at rest" and "rod at velocity v".) I know the voltage (because I've selected L and v and B to equal 1 volt). But the other two variables are unknown.

I need to see a worked-out example. Preferably three (or six examples) corresponding to the three diagrams above (at rest and in action). Make whatever additional assumptions you need to. Thanks.

 

[Jeff Rosenbury]

Fine.

Suppose the rods are 10cm square and 1m long. Let's say they are 1m apart.

We plug the numbers in our handy capacitance calculator and get 0.88 pF. That doesn't count the "leads" leading to the resistor or the cross bar (which is just a small value resistor). This will cause some fringing and the like. But I'm too lazy to figure that. I'll stick to the plate calculator.

Another example, suppose the rods are 10m by 10m and 1mm apart; that's 0.88µF.

Let's get wild and include a titanium dioxide dielectric. Not we get 70µF.

BTW, I messed up the link to the tube datasheet.

 

[Gerry Rzeppa]

Suppose the rods are 10cm square and 1m long. Let's say they are 1m apart.
We plug the numbers in our handy capacitance calculator and get 0.88 pF.

1. Okay, so 0.88 pf which is 8.8e-13 farads. And let's say V=LvB= 1 volt. Then q=CV=8.8e-13*1 coulombs or about 5.5 million excess (or deficit) electrons. Yes?

Now let me try to wrap my head around what's happening here.

2. I find when I make the rails 10 times longer, the capacitance is multiplied by 10 (as we'd expect due to the larger plate area), and the number of electrons also increases by a factor of 10 (55 million now, instead of just 5.5 million). This makes sense since we have 10 times the space ("plate area") to work with -- the mutual repulsion of the electrons on the top plate (and the attraction to protons with a deficit of electrons on the bottom plate) will not be felt as strongly as before until we have 10 times as many electrons as before. Yes?

3. I also find that when I leave the length as it was but make the space between the rails 10 times smaller, the capacitance is again multiplied by 10 and the number of electrons goes up by a corresponding factor of 10. This also makes sense to me, at least capacitance-wise: we can now have 10 times the number of electrons on the top plate because the mutual repulsion of electrons there is offset by the stronger attraction of the much closer positively charged bottom plate. Yes?

Unfortunately, I'm having trouble picturing point (3) above, circuit wise. Consider these three circuits (each with just a battery, a bulb, and some wire):

Let's say we've adjusted everything so the bulb will light with 1 volt, and the capacitance between that top wire and the bottom wire in the left circuit is about 0.88 pf, as above. That would mean we need an excess of about 5.5 million electrons on the top rail to make the thing work. So far, so good.

Now the center circuit is the same except the top and bottom rails are five times as long. Which means the capacitance is now five times greater and that means we need five times more electrons, 27.5 million, to make it work. Which is nevertheless understandable: we've got five times the "space" in those wires, so to get the same "pressure differential" we're going to need five times the number of excess/deficit electrons. Still good.

But now comes the problem. The right circuit is the same as the first except those top and bottom plates are now five times closer to each other, which again gives us five times the capacitance -- and thus the need for five times the number of electrons to make the circuit work. That makes no sense to me. I can see how this circuit makes a better capacitor than the other two; but I can't see why it should take five times the number of electrons to maintain a 1-volt differential between the top and bottom legs of the circuit.

Frankly, this anomaly makes me think the whole "capacitance approach" to the problem is not right. And not only for the reason just stated. It also seems odd to me that the current through that bulb might be as large as 6.2e+18 electrons per second, yet mere millions of electrons are involved in determining the voltage. Seems way out of proportion.

 

[Jeff Rosenbury]

It makes sense to me.

The electromagnetic force is very strong. Electrons don't weigh much. It takes far fewer of them to make charge than it takes for that charge to move them.

But it really doesn't matter what we think. The universe acts as it wants. It pays no attention to our opinions.

 

[mfb]

I can see how this circuit makes a better capacitor than the other two; but I can't see why it should take five times the number of electrons to maintain a 1-volt differential between the top and bottom legs of the circuit.

Those two statements are exactly the same, by the definition of capacitance. How can one be unclear while the other one is clear?

It also seems odd to me that the current through that bulb might be as large as 6.2e+18 electrons per second, yet mere millions of electrons are involved in determining the voltage. Seems way out of proportion.

You don't need any surplus of electrons anywhere for motion. Many electrons (something like 10²⁶ per kilogram of conductor) contribute to the current, having a few millions more or less does not make any difference.
If you calculate the drift velocity of electrons in conductors, you'll typically get something of the order of millimeters per second.

 

[Gerry Rzeppa]

It makes sense to me.

Then help me to make sense of it. Why should the circuit on the right require five times the number of excess/deficit electrons than the circuit on the left to maintain the same voltage differential across the bulb?

 

[Gerry Rzeppa]

You don't need any surplus of electrons anywhere for motion.

Do I need surplus electrons anywhere for voltage? Or are you still implying that the description of motional EMF at the top of this thread should be modified to read more like this (implied modifications in bold):

"The magnetic force acting on a free electron in the rod will be directed upwards. As a result, an insignificant number of electrons will start to accumulate at the top of the rod. The charge distribution of the rod will therefore change, but not in any significant way, and the top of the rod will have an insignificant excess of electrons (negative charge) while the bottom of the rod will have an insignificant deficit of electrons (positive charge). This excess/deficit of electrons will not result in a potential difference between the ends of the rod equal to LvB, though the potential difference will be equal to LvB due to other unspecified considerations."

 

[mfb]

Do I need surplus electrons anywhere for voltage?

Yes (in equilibrium), but you don't need voltage for current. Superconductors can have currents without any potential difference.

 

[Gerry Rzeppa]

Yes (in equilibrium), but you don't need voltage for current. Superconductors can have currents without any potential difference.

Okay, thanks. I don't think my ten-year-old will be running into any superconductors in his vacuum-tube guitar amp. The things run much too hot for that!

 

[Gerry Rzeppa]

The electromagnetic force is very strong...

I'd like to go back for a minute to the original illustration because I don't see how we calculate the capacitance (and thus the number of displaced electrons) in this case:

There appears to be only one "plate" -- unless we consider the copper between the top and bottom of the rod the dielectric. But the dielectric constant of metals is near infinity (I'm told), so that will give us a ridiculously large capacitance (and thus a ridiculously large number of displaced electrons). Help!

 

[Jeff Rosenbury]

Copper has a dielectric constant of about 6. (http://deltacnt.com/99-00032.htm )

Next we need to determine the charge distribution. A linear distribution seems like a reasonable guess. Most of the charge carriers are near the ends and the middle is neutral.

Now we integrate over the length of the rod with the voltage moment of "inertia" (which is properly called the "voltage moment" I think). That's the average voltage at each area of the differential length element. (We don't actually use the voltage yet except to solve a singularity problem.)

½L
∫ 6ε_ºA/2l dl = C ≅ 3ε_ºA ln (½L).
0

I played fast and loose with the integral. ln(0) is infinite and thus undefined, but the voltage goes to zero there (faster than a log function) so I think that's o.k. (Remember capacitance is defined by charge, which must be zero for zero voltage.) Perhaps someone could correct my maths? It's been a while since college.

We need to run another integral including voltage for the total charge since it is a function of length as well. I'll leave that to someone else.

The formula makes sense because the capacitance of the region near the center is contributes much more than more distant regions, just like a log function.

I do question my source for the dielectric constant. It was for a catalyst which might be powder. To be thorough we would run tests and confirm a value. I'm thinking a test where we moved a copper rod at a constant speed through a uniform magnetic field then counted the electrons might work.

 

[Gerry Rzeppa]

Copper has a dielectric constant of about 6. (http://deltacnt.com/99-00032.htm )... I do question my source for the dielectric constant. It was for a catalyst which might be powder.

Yeah, I'm not buying that one. Looking around in books and on the web the consensus appears to be that the dielectric constant for conductors is infinity. Here, for example, is a clip from a book called, Comprehensive Physics:

And here's a similar argument from a paper on the web (bold highlight mine):

"In E&M, we learned the famous formula for dielectric materials: D(r) = ε E(r). D is the electrical displacement, which is related to the electric field caused by the free moving charge (the externally added charge). E is the electric field caused by the total charge, which includes the free moving and the bound charge (the internally induced charge). ε is the dielectric constant, also called permittivity, which relates the D to E. ε is infinite for metals in the limit where the applied field is spatially uniform. In this case, the electrons inside the metal are free to arrange themselves until their own electric field exactly counters the externally applied field D. Thus, the total field E becomes 0."

So how do we apply the "capacitance approach" in this case?

And I'm still wondering about my earlier question: Why should the circuit on the right require five times the number of excess/deficit electrons than the circuit on the left to maintain the same voltage differential across the bulb?

I have no idea how I would explain that to a kid. I understand that there is capacitance involved in all three configurations; I'm simply have trouble believing it's significant in any of the three cases. Makes it sound like what's going on between the wires is more important that what's going on inside the wires.

 

[Jeff Rosenbury]

Yeah, I'm not buying that one. Looking around in books and on the web the consensus appears to be that the dielectric constant for conductors is infinity. Here, for example, is a clip from a book called, Comprehensive Physics:

You are looking at the case of a perfect electric conductor (PEC) like a superconductor. In a PEC there is no electric field. The entire field is canceled by eddy currents since there is no resistance. Yet in normal metals there is some limited resistance. That resistance slows eddy currents and allows a field to form. So the logic of "No field, no ε" doesn't hold.

And here's a similar argument from a paper on the web (bold highlight mine):

"In E&M, we learned the famous formula for dielectric materials: D(r) = ε E(r). D is the electrical displacement, which is related to the electric field caused by the free moving charge (the externally added charge). E is the electric field caused by the total charge, which includes the free moving and the bound charge (the internally induced charge). ε is the dielectric constant, also called permittivity, which relates the D to E. ε is infinite for metals in the limit where the applied field is spatially uniform. In this case, the electrons inside the metal are free to arrange themselves until their own electric field exactly counters the externally applied field D. Thus, the total field E becomes 0."

From above: "in the limit where the applied field is spatially uniform". Your applied field is not uniform. You have somewhat artificially set up a case where the underlying assumptions don't apply. Now you are using arguments based on those assumptions.

Capacitance is a defined quantity. It is defined as the charge divided by the voltage. You are arguing that this isn't the case. Well there's nothing wrong with that argument. As Lewis Carol wrote: "'When I use a word,' Humpty Dumpty said in a rather scornful tone, 'it means just what I choose it to mean -- neither more nor less.'" But don't expect others to agree with you or even understand you.

The answer to why a smaller circuit requires more electrons is because the electric field falls off with distance. Remember those electrons have paired protons somewhere. When the proton is near, it partially cancels the effects of the electron. When it's far, not so much.

You are correct that the capacitive approach may not be the best to solve this problem. I feel the lack of reliable ε measurements for metals make it problematic. Experimental data should be obtained. The test set up I envision would want a PEC to count the electrons across the small (differentialish) elements. Also, the value of ε might depend on the geometry (and temperature). (Remember ε is also a defined value. It relates the electric displacement with the electric field -- very similar to capacitance. There is no requirement that the number be a simple real value.)

For what it's worth, this would make a great science project/thesis (if it hasn't been done yet).

 

[Gerry Rzeppa]

Capacitance is a defined quantity. It is defined as the charge divided by the voltage... You are correct that the capacitive approach may not be the best to solve this problem. I feel the lack of reliable ε measurements for metals make it problematic.

I agree, but I don't think it's just the lack of reliable ε measurements in this case. The eggs-sitting-on-the-wall at Wikipedia describe a capacitor as: "two conductors separated by a non-conductive region. The non-conductive region is called the dielectric." In this case, there is no non-conductive region, hence no dielectric, hence no dielectric constant. Further, it says, "A capacitor is assumed to be self-contained and isolated, with... no influence from any external electric field." Hardly the case in this example. Finally, it says, "the dielectric develops an electric field," which, again, doesn't apply in this case because we have no dielectric.

The answer to why a smaller circuit requires more electrons is because the electric field falls off with distance. Remember those electrons have paired protons somewhere. When the proton is near, it partially cancels the effects of the electron. When it's far, not so much.

I understand that is the theory. But I wonder if, in practice, it has the significant effect that your suggesting. A decent capacitor must be precisely constructed; we can't just take a couple of flexible wires and place them relatively close to each other and expect to experience the kind of effects that the formulas suggest. There are simply too many imperfections (to put it mildly) in the geometric configuration.

I'm not really sure where to go from here in this discussion.

 

[mfb]

The concept of a capacitance is much more general than the electronic component "capacitor". I still think we need separated entities to define capacitance, something like a continuum capacitance function (how would that look like?) would be ... interesting.

 

[sophiecentaur]

The ultimate goal is to explain the workings of a basic vacuum tube guitar amp circuit to a ten-year-old in electron-flow terms.

I am truly sorry but I find that statement very disturbing. You are here on PF trying to get together a very personal view about Electricity, which is , from what I have read, full of misconceptions and you are actually contemplating passing these on to a tender young brain. Have pity on the child and buy him / her a book on Science, which will (probably) have correct ideas in it.
I have heard and seen some amazingly inappropriate stuff told to whole classrooms full of young kids by teachers with peripheral Physics Education, themselves, and who just don't 'get' Electricity. It really isn't fair on the poor little things. Leave it to the experts if you want your ten year old to get the right story.

PS, my Dad gave me that self same talk when I was about that age. But he knew his stuff. I took it on board and never forgot it.

 

[Gerry Rzeppa]

Okay, let's try this one:

I charge up a capacitor (value discussed below) to 1 volt and then insert it as shown in the circuit above. The resistor is 1 ohm, so the current is initially 1 amp. A larger capacitor will maintain the flow longer, but will not increase the voltage. The voltmeter shows the voltage starting at 1 volt and dropping from there. It seems to me:

1. That the voltage between A and B is related to the ratio of excess/deficit electrons on the top/bottom of this circuit. Yes?

2. That the number of excess/deficit electrons may be substantial. For example, if the capacitor is large enough to sustain a 1-amp flow for 1 second, then the number of excess electrons must have been at least 6.2e18 at the start. Yes?

3. That a larger capacitor can maintain the 1-volt reading longer, not because the ratio of excess/deficit electrons is different, but simply because it takes longer to move enough electrons to significantly change that ratio. Yes?

So far so good? I hope so. Now for the $64,000 question:

4. What's the relationship between the various ratios of excess/deficit electrons that exist in this circuit at various points in time, and the voltage readings we see on the meter?

 

[sophiecentaur]

Okay, let's try this one:

View attachment 86841
I charge up a capacitor (value discussed below) to 1 volt and then insert it as shown in the circuit above. The resistor is 1 ohm, so the current is initially 1 amp. A larger capacitor will maintain the flow longer, but will not increase the voltage. The voltmeter shows the voltage starting at 1 volt and dropping from there. It seems to me:

1. That the voltage between A and B is directly related to the ratio of excess/deficit electrons on the top/bottom of this circuit. Yes?

2. That the number of excess/deficit electrons may be substantial. For example, if the capacitor is large enough to sustain a 1-amp flow for 1 second, then the number of excess electrons must have been at least 6.2e18 at the start. Yes?

3. That a larger capacitor can maintain the 1-volt reading longer, not because the ratio of excess/deficit electrons is different, but simply because it takes longer to move enough electrons to significantly change that ratio. Yes?

So far so good? I hope so. Now for the $64,000 question:

4. What's the relationship between the various ratios of excess/deficit electrons that exist in this circuit at various points in time, and the voltage readings we see on the meter?

That's a really good example of how an alternative, personal model of Electrical Circuit Operation really doesn't help. If you want to talk about electrons in this context then you have to talk Quantum Mechanics and Statistics. This is why EE is taught in terms of Charge and Current. Only when you are fully conversant with the standard approach to EE theory can you afford to get into the questions you seem to be wanting to ask for starters.

 

[Gerry Rzeppa]

I am truly sorry but I find that statement ["The ultimate goal is to explain the workings of a basic vacuum tube guitar amp circuit to a ten-year-old in electron-flow terms."] very disturbing. You are here on PF trying to get together a very personal view about Electricity, which is, from what I have read, full of misconceptions and you are actually contemplating passing these on to a tender young brain...

On the contrary, my questions here are an attempt to clarify my understanding so I don't pass misconceptions on to the little guy. The way you and others can help is to simply answer the questions I ask, in the order asked, stopping (with an explanation) when an error is found.

This is the kid we're talking about (he's a bit older now):

This is the "No-Solder Banana Jack Amplifier Kit" I've developed for the course:

This is our text ("The clearest and most entertaining introduction to basic electronics ever written," https://www.amazon.com/dp/0962781592/?tag=pfamazon01-20):

And the four questions I'm working on at the moment appear below:

I charge up a capacitor to 1 volt and then insert it as shown in the circuit above. The resistor is 1 ohm, so the current is initially 1 amp (assuming a sufficiently large capacitor). The voltmeter shows the voltage starting at 1 volt and dropping from there. It seems to me:

1. That the voltage between A and B is related to the ratio of excess/deficit electrons on the bottom/top of this circuit. Yes?

2. That the number of excess/deficit electrons may be substantial. For example, if the capacitor is large enough to sustain a 1-amp flow for 1 second, then the number of excess electrons must be at least 6.2e18 at the start. Yes?

3. That a larger capacitor can maintain the 1-volt reading longer, not because the ratio of excess/deficit electrons is different, but simply because it takes longer to move enough electrons to significantly change that ratio. Yes?

4. What's the relationship between the various ratios of excess/deficit electrons that exist in this circuit at various points in time, and the voltage readings we see on the meter?

[Please refrain from replying unless you have specific answers to the specific questions asked; extraneous posts only make it difficult for others to find the most recent unanswered questions. Thanks.]

 

[sophiecentaur]

1. That the voltage between A and B is related to the ratio of excess/deficit electrons on the bottom/top of this circuit. Yes?

Q=CV

That the number of excess/deficit electrons may be substantial. For example, if the capacitor is large enough to sustain a 1-amp flow for 1 second, then the number of excess electrons must be at least 6.2e18 at the start. Yes?

Q=∫Idt over the limits t →0

That a larger capacitor can maintain the 1-volt reading longer, not because the ratio of excess/deficit electrons is different, but simply because it takes longer to move enough electrons to significantly change that ratio. Yes?

4. What's the relationship between the various ratios of excess/deficit electrons that exist in this circuit at various points in time, and the voltage readings we see on the meter?

Q=Q₀ Exp(-t/RC)

If you approach it this way then the verbal description / arm waving can be checked against the formulae. Science without some Maths is, imo, a waste of time. The ancients found this during the Enlightenment period.

 

[Gerry Rzeppa]

Q=CV... Q=∫Idt over the limits t →0... Q=Q₀ Exp(-t/RC)... Science without some Maths is, imo, a waste of time...

Thanks for the specific answers. You are obviously an intelligent, educated, and well-spoken person. Unfortunately, your answers are of little use to me. I'm not looking for formulas that are beyond the kid's reach. I'm looking for plain English descriptions of how the electrons behave in the circuit, and how that behavior is related to what the kid sees on the scope and his multi-meter.

I understand the critical role of mathematics in science -- I have a degree in mathematics myself. But having spent most of my adult life teaching children (I'm now 62), I have developed a firm conviction that the human brain learns best when it is fed pictures before words, and words before formulae.

If you approach it this way then the verbal description / arm waving can be checked against the formulae

Actually, the "checking" should go both ways. Errors can easily slip through the cracks between pictures and words, to be sure. But formulae can also be easily misunderstood and misapplied (as when a kid thinks there cannot be a potential difference across an open switch, because V = IR, and if there is no I there cannot be any V; or when a kid agrees, on theoretical grounds, that the current leaving a light bulb has to be equal to the current entering the bulb, but argues that the current in the bulb filament itself has to be much less, since V = IR, and the bulb filament has more R than the neighboring wires so it must have less I). It thus takes all three to really get an idea into a kid's head: pictures, words, and formulae -- in that order. I'm working on the pictures and words here.

Want to try again?

I charge up a capacitor to 1 volt and then insert it as shown in the circuit above. The resistor is 1 ohm, so the current is initially 1 amp (assuming a sufficiently large capacitor). The voltmeter shows the voltage starting at 1 volt and dropping from there. It seems to me:

1. That the voltage between A and B is related to the ratio of excess/deficit electrons on the bottom/top of this circuit. Yes?

2. That the number of excess/deficit electrons may be substantial. For example, if the capacitor is large enough to sustain a 1-amp flow for 1 second, then the number of excess electrons must be at least 6.2e18 at the start. Yes?

3. That a larger capacitor can maintain the 1-volt reading longer, not because the ratio of excess/deficit electrons is different, but simply because it takes longer to move enough electrons to significantly change that ratio. Yes?

4. What's the relationship between the various ratios of excess/deficit electrons that exist in this circuit at various points in time, and the voltage readings we see on the meter?

 

[sophiecentaur]

Unfortunately, your answers are of little use to me. I'm not looking for formulas that are beyond the kid's reach.

I'm looking for plain English descriptions of how the electrons behave in the circuit, and how that behavior is related to what the kid sees on the scope and his multi-meter.

Well, this is the problem. You are trying to tell people about things that are bound to be beyond their understanding (which is why such things are usually taught to more mature students). You seem to think that talking in terms of 'electrons' makes the subject more accessible. Bearing in mind that they (and even you) have a limited appreciation of the behaviour of electrons - particularly when they are in a metal, I suggest that an alternative description is less likely to confuse their take on Physics. I could suggest the term "Charge" would be good, for a start. It has satisfied Engineers and Scientists at all levels for generations. If you insist on presenting your own model then you are 'on your own' (also true when people try other personal approaches to Science). The very fact that you are asking for step by step help in justifying your model, shows that it is not in a state to present to school kids.
You may feel that my reaction is over the top. But I have spent many hours of 'remedial' work to put right the misconceptions that A level students have gained from their previous Science teaching in lower school. Kids need consistency. Please wait until your ideas have been truly tested against accepted theories before you unleash them on young minds. It is essential that you should learn the basics of what you present thoroughly. Until then, I recommend that you stick to the limits of the curriculum (flawed as it may be).

What they see on a scope is a nice concrete experience for them, which they may remember for the rest of their lives. Formal thought does not develop for several years and the concepts involved in Electricity theory are very very Formal. If you think that your method will work then perhaps you should devise a test, to determine just what they have gained from your intended lessons. The results you get back could be revealing.

 

[Jeff Rosenbury]

Q=CV means the charge (in this case electrons) is equal to the voltage times some value we call the capacitance. The capacitance is defined by this equation. Now you might question just what capacitance is, but this equation is correct -- by definition.

If you start with a capacitor at 1 V through a resistance of 1Ω, an instant later, the voltage will no longer be one volt and the current will no longer be 1 Amp. That should be obvious to someone with a degree in mathematics. Since you have been teaching children for many years, I can understand your calculus being a bit rusty, but even so you should be able to grasp that if Q=CV and Q drops while C remains constant, V must drop as well. And since V=IR, and V is dropping (with R remaining constant) I must drop as well. So there is no capacitor value large enough to do as you claim.

In Electrical engineering we use a concept called the RC time constant. Basically the value τ=RC gives the time for a capacitor to discharge by ≈63%. This acts as a half-life function (actually a 63%-life function) with the capacitor discharging an additional 63% every τ. Tau can be made larger by increasing either R or C or both. But under nearly all circumstances the voltage and current start to fall instantly. (The major exception is when the resistance is variable such as in a transistor, tube, or other gain providing device.)

Finally, isn't there some unwritten rule (or perhaps a written one) about posting the pictures of minors on public forums? This kid could grow up to join a biker gang and be terribly embarrassed about his good grades as a child. The internet is forever.

 

[sophiecentaur]

Q=CV means the charge (in this case electrons) is equal to the voltage times some value we call the capacitance

I deliberately left out the 'explanations' to my equations because, without knowing what they satnd for and all the associated background, trying to compose a model of Electricity is a hopeless task. Scientists use equations because that is basically the only way they can communicate and make progress. A waving arm can cover less than one metre squared.

 

[sophiecentaur]

Finally, isn't there some unwritten rule (or perhaps a written one) about posting the pictures of minors on public forums? This kid could grow up to join a biker gang and be terribly embarrassed about his good grades as a child. The internet is forever.

I think it's a matter of honi soit qui mal y pense, quite frankly. We spend too much time second guessing things these days. That picture was a breath of fresh air afaiac.
If he joins a biker gang he can always say "My name is Sue, how do you do."

 

[Gerry Rzeppa]

You are trying to tell people about things that are bound to be beyond their understanding...

I think that describes pretty much everything. We don't fully understand how sunflowers grow, but that didn't stop the kid from growing one this summer and from grasping the "great circle of life" -- seed to plant to flower to seed, nor did it stop him from grasping the fact that the sunflower must be made mostly of water and air since the seed was tiny and the flower big and we didn't see that much decrease in the amount of soil "consumed." I'm pretty sure a guitar amp can be explained at that sort of level.

You seem to think that talking in terms of 'electrons' makes the subject more accessible.

Yes. No kid I have ever known has had trouble with the electron-flow description of a vacuum tube. But lots of them have trouble with the proper application of Ohm's Law (as illustrated in my previous post).

Bearing in mind that they (and even you) have a limited appreciation of the behaviour of electrons - particularly when they are in a metal, I suggest that an alternative description is less likely to confuse their take on Physics. I could suggest the term "Charge" would be good, for a start.

If I was interested in making things up, I'd simply stick with Amdahl's "greenies."

The very fact that you are asking for step by step help in justifying your model, shows that it is not in a state to present to school kids.

Granted. But that doesn't mean I should abandon it. It means I should keep pursuing it until either (a) it is ready for the kid, or (b) I become convinced that it's making things harder rather than easier. So if you're really interested in the kid's welfare, and you think abandoning the electron-flow perspective is the thing to do, help me get to (b) as quickly as possible -- by simply answering the questions I'm asking. I may be more unconventional and persistent than the average person, but I'm neither stupid nor stubborn.

Please wait until your ideas have been truly tested against accepted theories before you unleash them on young minds.

As I said before, that's exactly what I'm doing right here, right now.

If you think that your method will work then perhaps you should devise a test, to determine just what they have gained from your intended lessons. The results you get back could be revealing.

I have performed a preliminary test. I gave my wife (who knows nothing about electricity) a standard basic text on electrons, and Amdahl's book. She quickly rejected the standard text, but couldn't stop reading Amdahl's work. And, thanks to that, she is now able to understand these posts when I print them off and discuss them with her. So it seems to me that Amdahl was on the right track when he wrote his book. I'm simply trying to fill in a couple of the blanks in his presentation.

Scientists use equations because that is basically the only way they can communicate and make progress.

That's just silly. Anything that can be expressed in a formula can be equivalently expressed in a sufficiently complete natural language. The one may be more concise and convenient at certain times, but the reverse may be true at other points. Sometimes a picture (or a formula) is worth a thousand words, sometimes it's the other way around. Pictures, words, and formulae are all necessary for effective communication. Consider, for example, this page from one of Einstein's notebooks, where he was trying to get his thoughts down in the most concise and effective manner:

Note that he naturally and intuitively uses all three tools.

 

[sophiecentaur]

Anything that can be expressed in a formula can be equivalently expressed in a sufficiently complete natural language.

Now that really is silly. You clearly don't appreciate the advanced Maths that is necessary to describe even a simple servo loop. The fact is that Maths is just the complete natural language that's called for.

Einstein's name frequently comes up as someone who did things just by intuition and who couldn't do Maths. Both are misconceptions. He used rigorous Maths to arrive at his conclusions. I can't read that attachment because it stays the same size whatever I do but his note books were intended for his personal use and you can have no idea about what messages were there for him to understand.

How would you know how much your wife 'understands' of these posts if she has rejected standard texts in favour of a very entertaining book? She is not in a position to understand anything abut the validity of what Amdahl's book says and it would be unfair to subject her to the sort of questions that even a simple electrical circuit would present. Entertainment is not synonymous with basic learning - even if it is fun.

You seem to think that your alternative approach to things is valid and sufficient, which suggests to me that you probably have not had a vast experience of the conventional approach. This boring and lacklustre regime has been responsible for all the advances in the Physical Sciences and in Engineering since Gallileo. That sort of convinces me that it has a certain worth. What evidence do you have that your approach could achieve the same?

 

[Gerry Rzeppa]

If you start with a capacitor at 1 V through a resistance of 1Ω, an instant later, the voltage will no longer be one volt and the current will no longer be 1 Amp. That should be obvious to someone with a degree in mathematics. Since you have been teaching children for many years, I can understand your calculus being a bit rusty, but even so you should be able to grasp that if Q=CV and Q drops while C remains constant, V must drop as well. And since V=IR, and V is dropping (with R remaining constant) I must drop as well. So there is no capacitor value large enough to do as you claim.

Excellent point. I stand corrected. I was only trying to establish that the number of electrons we're talking about may be in the 10¹⁸ range and not mere millions, even in ordinary circuits. I'll reword that point after I get answers to some similar questions regarding a simpler configuration, below.

The pictures below show two capacitors (little and big) in various states of "charge". (The blue dots are not individual electrons, but large yet equal masses of free electrons; the arrangement of the dots is not literal, but figurative for easy counting):

The caps on the left (little and big) are uncharged -- the number of free electrons is equal top and bottom. The caps in the middle are charged, but not to capacity. The caps on the right are more fully charged, but still not quite to capacity. The charging process, it can be easily seen, is a matter of pulling electrons from the top of each capacitor and and pushing an equivalent number of electrons into the bottom of each.

Based on those pictures, I think the kid will be able to see:

1. That the voltage between the top and the bottom of these capacitors is directly related to the ratio of free electrons on the top and bottom of a cap. (The ratio, not the absolute number of electrons: the bottom left drawing has more electrons on the bottom, and twice as many altogether, than the top right drawing; yet the voltage is greater in the top-right capacitor because the ratio, bottom-to-top, is greater.) Yes?

2. That it takes more electrons to charge up a large capacitor to the same voltage level as a small capacitor. A large capacitor will therefore discharge more slowly than a small capacitor, all other things being equal. Yes?

3. That for any given ratio the voltage will be the same, no matter how big or small the capacitor. And vice-versa: for any given voltage, the ratio will be the same, no matter how big or small the capacitor. Yes?

So we've got some nice pictures and some meaningful words to go with them. What's needed is a formula to complete the set. We know that q=C/V (correction V=q/C), but based on point (3) above, it seems we ought to be able to relate q to V without mentioning C. The NEETS (Navy Electricity and Electronics Training Manual) says the relationship is this (http://www.tpub.com/neets/book1/chapter1/1k.htm):

""A difference of potential can exist between two points, or bodies, only if they have different charges. In other words, there is no difference in potential between two bodies if both have a deficiency of electrons to the same degree. If, however, one body is deficient of 6 coulombs (representing 6 volts), and the other is deficient by 12 coulombs (representing 12 volts), there is a difference of potential of 6 volts. The body with the greater deficiency is positive with respect to the other."

My problem with that statement is that it doesn't appear to take the ratio idea into account: it would make the large cap in the center of my drawing have a voltage equal to the rightmost small cap (since both have a difference of 4 globs of electrons).

Amdahl, I think, explains it better:

"Voltage is the reason electrons move... It's a percentage thing. It's the ratio between two charges. If there are 10 times as many electrons one place as another, it will have certain voltage, whether you're talking about 10 electrons or a million electrons."

Thoughts?

 

[analogdesign]

Amdahl, I think, explains it better:

"Voltage is the reason electrons move... It's a percentage thing. It's the ratio between two charges. If there are 10 times as many electrons one place as another, it will have certain voltage, whether you're talking about 10 electrons or a million electrons."

Thoughts?

Are you sure this is right? Lots of practical circuits work on the basis of charge balance (or charge sharing). Imagine if you had an isolated capacitor of 1F with 1V across it. By definition the charge Q stored on the capacitor is 1C. Now if you magically moved the plates closer by a factor of two, now the capacitor would have a capacitance of 2F and the voltage would decrease to 0.5V since Q couldn't have possibly changed (remember this system is isolated). Where is the
ratio between two charges?" There is one charge. The charge on the capacitor.

Since you brought up Einstein earlier remember it was he who said "Everything should be made as simple as possible, but not simpler". The concepts of charge, current, and voltage are quite simple and they work. Very well.

 

[davenn]

We know that q=C/V,

No, that is incorrect, you missed what was told to you several times
Q=CV ( Q = C x V)

I have been reading through the thread several times ...
You came asking for help, and people have given you the better way to do this teaching to the kids,
but you still want to ignore that and go with your own way which, to be honest, I find more confusing than the correct way

Take a step back and a deep breath
and consider a better way, which won't lead to further confusion for them later in life if they decide to pursue electronics

Dave

 

[Gerry Rzeppa]

No, that is incorrect, you missed what was told to you several times
Q=CV ( Q = C x V)

You're right, I typed that in wrong. I've corrected it above.

You came asking for help, and people have given you the better way to do this teaching to the kids,
but you still want to ignore that and go with your own way which, to be honest, I find more confusing than the correct way.

I think, by "correct," you mean usual. Many people agree that the usual ways don't work as well as they should. Here are two interesting papers on the subject:

http://files.eric.ed.gov/fulltext/ED287730.pdf
http://www.matterandinteractions.org/Content/Articles/circuit.pdf

Clearly, some change of approach is called for.

 

[Gerry Rzeppa]

Imagine if you had an isolated capacitor of 1F with 1V across it. By definition the charge Q stored on the capacitor is 1V. Now if you magically moved the plates closer by a factor of two, now the capacitor would have a capacitance of 2F and the voltage would decrease to 0.5V since Q couldn't have possibly changed (remember this system is isolated). Where is the ratio between two charges?" There is one charge. The charge on the capacitor.

Excellent! What you've done (by magically moving the plates closer by a factor of two) is to change one of my little capacitors into one of my big capacitors -- but without changing the number of electrons. So the ratio stays the same. Like so:

So it's clearly not: (a) the absolute number of electrons that determines the voltage; we eliminated that earlier.

And now -- thanks to your little thought experiment -- we can say that it's not just (b) the ratio of electrons in one spot versus another.

So what is it? What's changed? Seems to me it's the concentration of electrons that has changed -- the number of electrons per cubic inch, or the number of free electrons per proton, or something like that. (There's obviously more room in the bottom of the larger capacitor and it thus would take less energy to cram five extra globs of electrons in there. Or, after the fact, we could say that the electrons on the right bottom are less compacted than the ones on the left bottom, and thus the mutual repulsion between them is less. Either way, the voltage will be lower.)

So it seems, then, that voltage must be (c) a measure of the relative concentration of electrons in two spots. Better?