I Motor driven pendulum - How to track its position?

[maxitaxi]

Hello,

On the image below is a test pendelum for rock wool production. The pendelum is driven by two induction motors. When the right motor makes one revolution, the left motor makes two revolutions. The motors are positionally locked (example: when the right motor is at 35.3° the left motor is at 70.6°). The above part works OK.

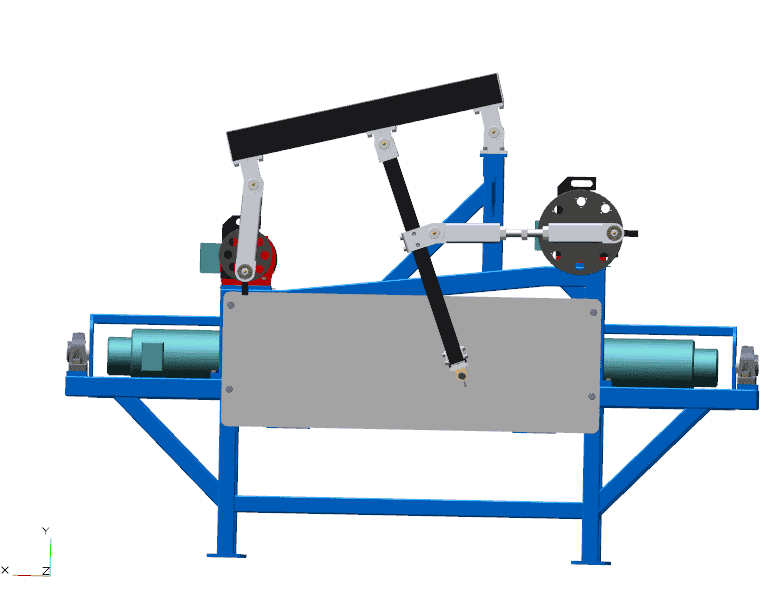
Currently we are using a simple analog procedure (marker and whiteboard) to plot the position of the pendelum (shown on the image below).

On the image below are the mesurements of the moving parts [mm]. The position of both motors at any given time is known. The speed at any given time is also known (nominal speed is 1500 rpm).

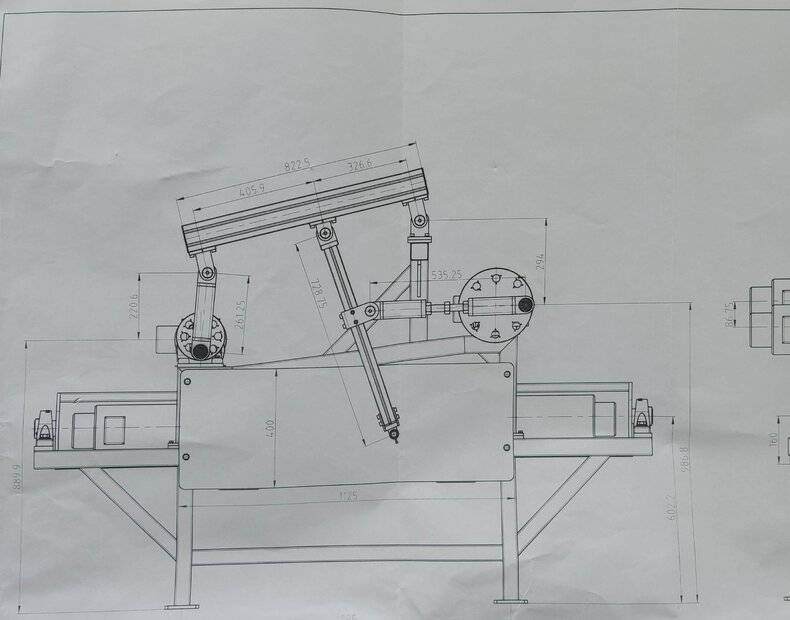
My question is how can movement of this sort of pendelum (where the marker is located) be described with equations. It would be a lot more transparent and easier to analyze to have the pendelum moevement data in digital form.

Thank you for your answer in advance.

Regards.

 

[jrmichler]

I once had a similar problem. It was to design a four bar linkage to follow a specific motion profile while minimizing peak acceleration. I wrote a program in Matlab with initial positions as inputs, and plots of position and acceleration as functions of input shaft position as outputs.

You have more links, but exactly one input (the second motor is geared to the first motor), and one output. It should be an easy program to write:

Start with the motor on the left.
Calculate position of motor crankpin.
Calculate position of pin between connecting rod and the top beam.
Calculate position of pin in middle of top beam.
Calculate position of crankpin of motor on the right.
Calculate position of pin connecting second motor connecting rod with pendulum.
Calculate position of end of pendulum.
Plot position of pendulum for one revolution of the slower motor.
(Optional) You can use numerical differentiation to calculate velocity and acceleration of the pendulum or any other point in the system.

Hint: It is good practice to plot the entire linkage at each step in the simulation. It slows the simulation down, but you get visual confirmation that the simulation is working properly. It is also helpful for debugging. And it's an excellent tool for showing other people how the mechanism works.

If you do not have Matlab, Octave (https://octave.org/) is Matlab compatible freeware. It's not quite as good as Matlab, but more than good enough for your application.