Move tricycle in circle during x sec at speed s

[transilvanian]

Homework Statement

I need to get a tricycle to move around a circle (depending on the angle of the front wheel) in MATLAB (but any mathematical formulae would help).
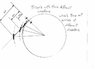
I have the variables: M (x, y, theta) which is the center point between the 2 back wheels and the angle of the tricycle, the angle phi of the front wheel, the speed in m/s and the duration in s.

Homework Equations

The instant center or rotation calculated from the position and angle of the front wheel.
http://en.wikipedia.org/wiki/Instant_centre_of_rotation

The Attempt at a Solution

This is what I got so far... and I am stuck.

function [x, y, theta] = MoveTricycle(M, phi, speed, duration)

front_wheel = [30*cos(M(3))+M(1) 30*sin(M(3))+Xt(2)];
distance = (v * dt)/2*pi;

alpha = 180-phi-90
radius = 30/cos(alpha);
ICR = [radius*cos(alpha*180/pi)+M(1) radius*sin(alpha*180/pi)+M(2)];
Angle_ICR = 180-90-alpha;front_wheel_after(1) = IRC(1) + cos(distance) * radius ;
front_wheel_after(2) = IRC(1) + sin(distance) * radius ;

% I need to find the position of M after the movement...
M = ?

I'm not even sure if the movement part is ok...
Thanks for your help

 

[Spinnor]

Does the following look like the right geometry?