Gargars
- 2
- 0
Hello everybody, I'm assigned to do particle physics home, which I don't really understant because I'm a freshman and I have choosen it as a free subject. Obviously, that was a mistake. I have been reading a book, but I'm not sure if I understand everything.
A particle of rest mass M, traveling at speed v in the x-direction, decays into two photons, moving in the positive and negative x-direction relative to the original particle. What are their energies? What are the photon energies and directions if the photons are emitted in the positive and negative y-direction relative to the original particle (i.e., perpendicular to the direction of motion, in the particles rest frame).
I previously solved an equation for particle decay products energies when parent particle is ant rest. These are E1=(M^2+m1^2-m2^2)/2M, and analogicaly for E2, just -m1 squered and +m2 squered.
I'm considering photon which is moving in the positive x-direction to have less energy than the other one. Maybe I should use relatyvistic velocity addition to find these energies?
There is another problem related to the previous one.
If a massive particle decays into photons, explain using 4-momenta why it cannot decay into a single photon, but must decay into two or more. Does your explanation still hold if the particle is moving at high speed when it decays?
The four-momentum:
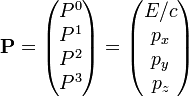
As far as I understand no particle can decay into another particle without nothing else. But that's not an explanation.
Homework Statement
A particle of rest mass M, traveling at speed v in the x-direction, decays into two photons, moving in the positive and negative x-direction relative to the original particle. What are their energies? What are the photon energies and directions if the photons are emitted in the positive and negative y-direction relative to the original particle (i.e., perpendicular to the direction of motion, in the particles rest frame).
Homework Equations
I previously solved an equation for particle decay products energies when parent particle is ant rest. These are E1=(M^2+m1^2-m2^2)/2M, and analogicaly for E2, just -m1 squered and +m2 squered.
The Attempt at a Solution
I'm considering photon which is moving in the positive x-direction to have less energy than the other one. Maybe I should use relatyvistic velocity addition to find these energies?
There is another problem related to the previous one.
Homework Statement
If a massive particle decays into photons, explain using 4-momenta why it cannot decay into a single photon, but must decay into two or more. Does your explanation still hold if the particle is moving at high speed when it decays?
The four-momentum:
The Attempt at a Solution
As far as I understand no particle can decay into another particle without nothing else. But that's not an explanation.