- #1
Jamesss
- 13
- 0
I posted this in the general forum but it probably belongs here.
This is a tricky one!
I'm unsure about the forces on the ground level.
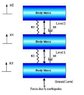
The problem is a 2-spring-damper system with three levels. A ground level, level 1 and level 2. Then a force is applied to the ground level simulating an Earth quake (eg the force could be sinusoidal). See the attachment for a diagram.
These are the forces I have resolved:
-level 2 mass:
gravitational force, m0*g (down)
Spring Force2, K1*(x1-x0) (up)
Damper Force2, b1*(x1'-x2') (up)
Inertial Force, m*x0'' (down)
-level 1 mass:
gravitational force, m*g (down)
Spring Force1, K1*(x2-x1) (up)
Damper Force1, b1*(x2'-x1')(up)
Inertial Force, m*x1'' (down)
Spring Force2, K1*(x1-x0) (down)
Damper Force2, b1*(x1'-x2') (down)
-level ground mass:
driving force (earthquake) = some function eg sine
g-force, mg (down)
Spring Force1, K1*(x2-x1) (down)
Damper Force1, b1*(x2'-x1')(down)
Inertial Force = m*x2'' (down)
I have tried to solve this using simulink, but for the positions of each level they fall towards negative oblivion. I am thinking I either have forgotten some force added too many.
Have I left anything out? *thinking*
James
This is a tricky one!
I'm unsure about the forces on the ground level.
The problem is a 2-spring-damper system with three levels. A ground level, level 1 and level 2. Then a force is applied to the ground level simulating an Earth quake (eg the force could be sinusoidal). See the attachment for a diagram.
These are the forces I have resolved:
-level 2 mass:
gravitational force, m0*g (down)
Spring Force2, K1*(x1-x0) (up)
Damper Force2, b1*(x1'-x2') (up)
Inertial Force, m*x0'' (down)
-level 1 mass:
gravitational force, m*g (down)
Spring Force1, K1*(x2-x1) (up)
Damper Force1, b1*(x2'-x1')(up)
Inertial Force, m*x1'' (down)
Spring Force2, K1*(x1-x0) (down)
Damper Force2, b1*(x1'-x2') (down)
-level ground mass:
driving force (earthquake) = some function eg sine
g-force, mg (down)
Spring Force1, K1*(x2-x1) (down)
Damper Force1, b1*(x2'-x1')(down)
Inertial Force = m*x2'' (down)
I have tried to solve this using simulink, but for the positions of each level they fall towards negative oblivion. I am thinking I either have forgotten some force added too many.
Have I left anything out? *thinking*
James