Penny57
- 7
- 3
- Homework Statement
- Operators can also be multiplied just like matrices. Physically, this represents applying two operations in succession. To compute in the abstract setting, we just need the rule ⟨i|j⟩ = δij .
(d) Compute the operator product of |1⟩⟨1| and |1⟩⟨1| + |2⟩⟨2|.
(e) Compute the operator product of |1⟩⟨2| + |2⟩⟨1| and |2⟩⟨2|.
- Relevant Equations
- O = O[SUB]ij[/SUB] |i⟩⟨j| = O[SUB]11[/SUB] * |1⟩⟨1| + O[SUB]12[/SUB] * |1⟩⟨2| + O[SUB]21[/SUB]|2⟩⟨1| + O[SUB]22[/SUB]|2⟩⟨2|.
For the first part of the problem, I managed to form this matrix;
=
However, that was because I was following this image;
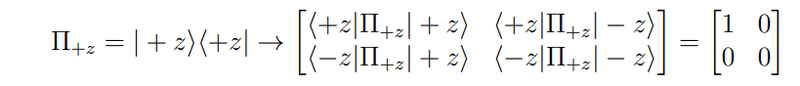
I'm not entirely sure how this was obtained, and I'm not really sure what to do to continue forward with part e. I apologize for my lack of knowledge - I've attempted to search for any youtube videos to help and go through online textbooks, but I'm unable to find what I am looking for.
| <1|O|1> | <1|O|2> |
|---|---|
| <2|O|1> | <2|O|2> |
=
| 1 | 0 |
|---|---|
| 0 | 0 |
However, that was because I was following this image;
I'm not entirely sure how this was obtained, and I'm not really sure what to do to continue forward with part e. I apologize for my lack of knowledge - I've attempted to search for any youtube videos to help and go through online textbooks, but I'm unable to find what I am looking for.