Multipole expansion of linearized field equations

[Stefaan Melis]

I read Chris Hirata's paper on gravitational waves (http://www.tapir.caltech.edu/~chirata/ph236/lec10.pdf) where he performs a multipole expansion of the gravitational source.
I got most of it, apart from the part where he expands the inverse distance function into a series :

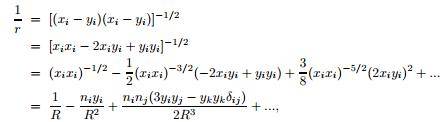
More specifically the second term in the last line, which should be positive according to me (product of 2 negative factors -1/2 and -2). Hirata finds a negative sign.
The sign is pretty important, since at the end of the paper he proves that the resulting gravitational wave is transversal by finding the vector product of the wave and the propagation vector to be zero. Which is indeed the case ... provided that the second term above is negative. Which, according to me, it isn't.
In no way I consider myself smarter than Chris Hirata, but here he lost me. And literature does not give me an answer.
Can anyone explain this sign ?

 

[vanhees71]

The 2nd term is due to the first-order Taylor-expansion term, i.e., it's
$$
\vec{y} \cdot \left [\vec{\nabla}_{y} \frac{1}{|\vec{x}-\vec{y}|}
\right]_{y=0}=\vec{y} \cdot \left [
\frac{-1}{|\vec{x}-\vec{y}|^2}_{\vec{y}=0}\;
\frac{\vec{y}-\vec{x}}{|\vec{y}-\vec{x}|} \right ]_{\vec{y}=0} =
+\frac{\vec{y} \cdot \vec{x}}{|\vec{x}|^3}=+\frac{\vec{y} \cdot \vec{n}}{|\vec{x}|^2}.
$$
i.e., you are right, it must be +. You find this also in many textbooks on classical electrodynamics (keyword: (Cartesian) multipole expansion).

You also see from the manuscript that it must be a typo when going from the pre-last line to the last!

 

[Stefaan Melis]

Thank you for confirming. That's too bad then, because it means that the calculation of the vector product at the end of the paper showing that the wave is transversal does not produce 0 :

The last 2 terms, both negative in the paper text, will then turn out to be positive, and cause the equation to become non-zero.

So I guess the series approximation does not allow to prove transversness in the way described above ? Too beautiful to be true ?

 

[Paul Colby]

Equation (1) is only valid in a Lorentz Gauge or

$\partial^\mu \bar{h}_{\mu \nu}=0$ (*)​

Although any coordinate transformation is valid to preserve (1) and (*) the coordinate function, $\xi^\mu$, are required to satisfy,

$\square \xi^\mu = 0$
​

and

$\partial^\mu \xi_\mu = 0$​

It's unclear to me that one may do the time transformation (36) independent of the spatial one (41) and still have these conditions (1) and (*) remain true?

 

[Paul Colby]

I've typed in Hirata's expression for $\xi_0$ Equation 36 and $\xi_j$ given in Equation 41 in Maxima. I then compute $\partial^\mu \xi_\mu$ and isolate the radiation terms (everything he's discussing is only in the far field where $1/r^n\approx 0$ for $n\gt 1$. I get,

$\partial^\mu \xi_\mu = \frac{\ddot{I}_{kk}}{2R} + O(1/r^2)$​

which isn't 0 as I think it must be. Equations 43 are the usual ones so the problem is likely in the details of Hirata's gauge change.

 

[Stefaan Melis]

Hi Paul ! Thanks for taking the time to give your feedback.

Personally I don't think there is an issue with the Lorenz gauge.
The only condition that a coordinate transformation needs to satisfy to remain within the Lorenz gauge is the wave equation (as explained in wikipedia : https://en.wikipedia.org/wiki/Gauge_fixing#Lorenz_gauge). The second equation that you mention (divergence of transformation function == 0) is not a requirement. It is unclear to me where you are getting this from ?
So any coordinate transformation that behaves as a wave function propagating at the speed of light (on the light cone) will respect the Lorenz gauge.
Hirata chooses his 2 additional coordinate transformations as the time integral of resp. the time-time and time-space components of the radiation terms, which are - per definition - wave functions on the light cone, and the time integral of a wave function is again a wave function.
So, to me, the 2 transformations fully respect the Lorenz gauge.

The only thing that still puzzles me is the initial statement of my post about the sign of the second term in the series expansion of the inverse distance function, which vanhees71 (thank you again for your confirmation !) and everyone else in literature finds to be positive, but is negative in Hirata's calculation. The negative sign is not just a typo, but is taken along all the way in the calculations and eventually proves that the radiation terms correspond to transverse and traceless gravitational waves. For educational purposes, this would have been a great result, but I feel unlucky not to be able to find it.
I even sent a mail to Chris Hirata asking for a clue, but I guess he is too busy to reply to these kinds of unsollicited messages.

Does anyone have a clue ?

 

[Paul Colby]

It is unclear to me where you are getting this from ?

My bad. MTW problem 18.2 page 438 says you're correct.

 

[vanhees71]

The only thing that still puzzles me is the initial statement of my post about the sign of the second term in the series expansion of the inverse distance function, which vanhees71 (thank you again for your confirmation !) and everyone else in literature finds to be positive, but is negative in Hirata's calculation. The negative sign is not just a typo, but is taken along all the way in the calculations and eventually proves that the radiation terms correspond to transverse and traceless gravitational waves. For educational purposes, this would have been a great result, but I feel unlucky not to be able to find it.
I even sent a mail to Chris Hirata asking for a clue, but I guess he is too busy to reply to these kinds of unsollicited messages.

Does anyone have a clue ?

Well, there are typos and misconceptions in textbooks and (more so) manuscripts, which often haven't been proof-read by somebody else than the author. Typing myself many texts of this kind, I can tell you that you don't see these typos yourself, if you haven't waited some time after typing the text. If you read an older of your own text carefully again, you'll often find typos of all kinds :-(.

So the lesson is to never trust anything, which you really want to use for your own research work, without carefully checking!

 

[Stefaan Melis]

Thank you for sharing your experiences. I fully agree with your statement.

It just feels strange that Hirata's paper was used as lecture notes of a GR class that he taught in 2012 at the Caltech. So a lot of students got this and used it for their study. Surely they must be the most critical reviewers and apparently never got it to be corrected...

 

[Paul Colby]

Just spit balling here, but how is the unit vector $n_i$ defined? Is it from the source to the observation point or from the observation point to the source. Easy to pick up a sign if you wish.

Edit: 100% convinced that $n_i=x_i/R$ as defined and the sign in the expansion is positive.