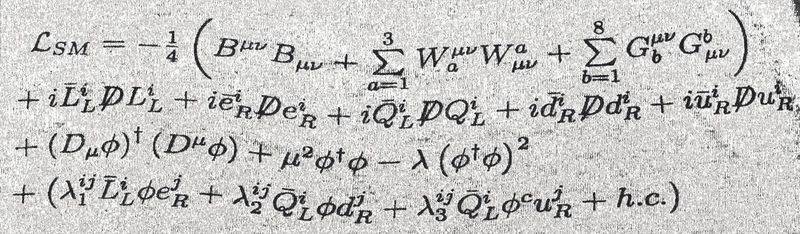SUMMARY
The discussion centers on the Lagrangian of the Standard Model of particle physics, specifically focusing on the roles of lines 2 and 4. Line 2 represents a kinetic term that describes interactions among leptons and quarks, while line 4 is an interaction term detailing the coupling of these particles with the Higgs field, incorporating Yukawa couplings. The conversation clarifies that neutrinos are massless within the Standard Model, and Fadeev-Popov ghosts are not included in this context. The importance of the covariant derivative for gauge invariance is emphasized, along with the concept of spontaneous symmetry breaking occurring in the gauge sector.
PREREQUISITES
- Understanding of the Standard Model of particle physics
- Familiarity with Lagrangian mechanics
- Knowledge of gauge invariance and covariant derivatives
- Basic concepts of quantum field theory
NEXT STEPS
- Study the role of Yukawa couplings in particle physics
- Learn about gauge fixing and Fadeev-Popov ghosts
- Explore the implications of spontaneous symmetry breaking in the Standard Model
- Investigate the mathematical formulation of the covariant derivative in gauge theories
USEFUL FOR
Physicists, graduate students in particle physics, and anyone interested in the mathematical foundations of the Standard Model and quantum field theory.