kambrian
- 4
- 0
I am having a problem with this question. I can't figure out how to approach it.
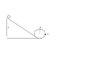
A solid sphere of mass m and radius r rolls without slipping along the track. it starts from rest with the lowest point of the sphere at height h above the bottom of the loop of radius R, much larger than r.
What are the force components on the sphere at he point P if h = 3R?
How would I go about solving this problem? I attached a picture of the situation.
A solid sphere of mass m and radius r rolls without slipping along the track. it starts from rest with the lowest point of the sphere at height h above the bottom of the loop of radius R, much larger than r.
What are the force components on the sphere at he point P if h = 3R?
How would I go about solving this problem? I attached a picture of the situation.