Need help finding magnitude of A - B + C given 3 vectors

[iadg87]

You are given three vectors.
A = 46.0 at θ1 = 56.6° above the +x axis
B = 25.0 at θ2 = 34.4° above the −x axis
C = 32.0 along the −y axis.Determine A - B + C (magnitude and angle from the positive x axis).
Determine the angle relative to the positive x-axis, positive above and negative belowI have attempted the solution many times and ended up with 44.6 and -9.96 deg. but it is incorrect

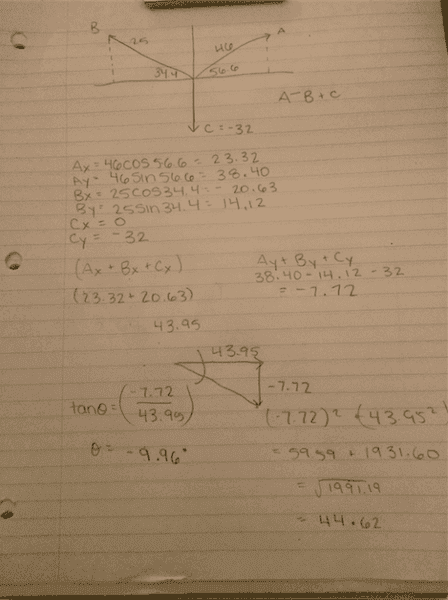
Any help would be appreciated!

Regards,

 

[brainpushups]

Looks like you've made a simple sign error. You have the correct sign for the vector B's components, but then you added the values for the resultant's x component rather than subtracting.