Finding the magnitude/direction of a resultant vector?

In summary, the conversation discusses four vectors A, B, C, and D with their respective magnitudes and angles with respect to the positive x axis. The question asks for the magnitude and direction of the resultant vector R when the parallelogram law is applied to A and B. The attempted solution uses the law of sines and law of cosines to find the magnitude and direction, but the results are incorrect. The expert suggests finding the components of each vector and adding them to find the resultant vector.
  • #1
anonymous812
10
0

Homework Statement


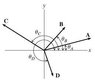
Four vectors A, B, C, and D are shown (not to scale). Vector A has magnitude 20.0 and acts at an angle of 12.9 degrees with respect to the positive x axis. Vector B has magnitude 15.0 and acts at an angle of 55.7 degrees with respect to the positive x axis. Vector C has magnitude 31.5 and acts at an angle of 146.5 degrees with respect to the positive x axis. Vector D has magnitude 13.0 and acts at an angle of 296.4 degrees with respect to the positive x axis.

Question: What are the magnitude and direction of the resultant vector, R, when the parallelogram law is applied to A and B?

Homework Equations


Law of Sines and Law of Cosines..
A/sina=B/sinb=C/sinc
C=sqrt(A^2+B^2-2ABcos(c)

The Attempt at a Solution



I solved for The resultant vector and got 32.6 N... R=sqrt(20^2 +15^2-2(20*15*cos(137.2)))
Then I used law of sines to find the direction and got 52.5 degrees.

Apparently, I'm wrong. I recalculated all the angles not given and they seem to be right, but my end result ends up being wrong. Any tips?
Thank you!
 

Attachments

  • MEng_SD_2-2-1_img1.jpg
    MEng_SD_2-2-1_img1.jpg
    4.6 KB · Views: 1,768
Physics news on Phys.org
  • #2
anonymous812 said:
Then I used law of sines to find the direction and got 52.5 degrees.

You might want to post more detail on what you did here. That's where the problem lies.
 
  • #3
Alright, sorry! I did 32.6/sin(r)=15/21.4.
I got 21.4 from the calculating the angle 1/2(ThetaB-ThetaA)
 
  • #4
It will be a lot easier to find the components of each vector, then add them component-wise, then find the magnitude and direction of the resultant.
 
  • Like
Likes 1 person
  • #5
Thanks! You're right that was easier. I got it :)
 

FAQ: Finding the magnitude/direction of a resultant vector?

1. How do you find the magnitude of a resultant vector?

The magnitude of a resultant vector can be found using the Pythagorean theorem, which states that the magnitude of a vector is equal to the square root of the sum of the squares of its components. In other words, if the resultant vector has components of x and y, its magnitude would be √(x^2 + y^2).

2. What is the direction of a resultant vector?

The direction of a resultant vector can be found using the inverse tangent function, or arctan, which is commonly written as tan^-1. The direction is given by the angle formed between the vector and the x-axis, and can be calculated as tan^-1(y/x).

3. What is the difference between magnitude and direction of a vector?

The magnitude of a vector refers to its size or length, while the direction refers to the angle at which the vector is pointing. Both magnitude and direction are necessary to fully describe a vector in two dimensions.

4. Can a resultant vector have a negative magnitude?

No, the magnitude of a vector is always positive. It represents the length of the vector without regard to its direction. If a vector has a negative direction, it simply means it is pointing in the opposite direction of a positive vector with the same magnitude.

5. How do you handle vectors with more than two components?

In three-dimensional space, vectors can have three components: x, y, and z. To find the magnitude of a resultant vector in this case, we use the formula √(x^2 + y^2 + z^2). To find the direction, we use the inverse tangent function twice: first to find the angle in the x-y plane, and then again to find the angle between the resultant vector and the x-y plane.

Similar threads

Vectors Directions: Where is this Resultant Vector Pointing?
Replies
14
Views
804
Finding the magnitude (length) and direction (angle) of a vector
Replies
2
Views
962
Vectors along different coordinate axes
Replies
2
Views
1K
Vector is a function of its position or not?
Replies
16
Views
1K
Resultant of two vectors of equal magnitude
Replies
3
Views
6K
Minimum and maximum resultant of three vectors.
Replies
4
Views
5K
Finding the resultant of three vectors
Replies
20
Views
11K
Calculate electric force using Coulomb's law (vector components are the struggle)
Replies
3
Views
571
2 unknown Forces+known resultant force
Replies
1
Views
1K
To find the magnitude of the resultant of forces around a triangle
Replies
4
Views
2K

Hot Threads

Recent Insights

Back
Top