Need Help with Bond Length Calculations of Acetylene

[Popz]

Homework Statement

I have done most part of the data analysis. I am stuck with rearranging the equation in the correct way.

Relevant Equations

see below

Hey!

I am trying to determine the bond length of acetylene by analysing the vibrational spectrum of both H-Acetylene and D-Acetylene. I was able to calculate both the rotational constant and the moment of inertia but am stuck now as to how I get to the correct solution.

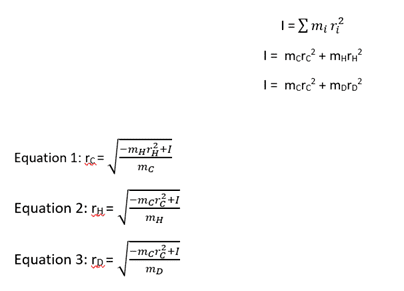
On the left is the original moment of inertia equation for polyatomic molecules which I have expanded to be specific for acetylene.
Then, on the right side are my rearrangements for the bond length of the respective molecules. I have been told that this is solvable by using two simultaneous equations - the moment of inertia for H and D. But I don't know how to solve this in practice.

However, I have been told that this is (probably) the correct equation. But I don't know how I get to this point.
I understand that the basic rearrangement equals r = √(I/2m) but, for example, I don't know why r(D) - r(H) would equal r(H) if that's what the first equation implies?​

Hope that's not too confusing.
Thanks!

 

[mjc123]

You are over-complicating things with your square-root equations. In the equations for the moments of inertia (label them I_H and I_D so you don't start thinking they're the same) you have two simultaneous linear equations in the unknowns r_C² and r_H² (assuming r_D = r_H). Solve for these and then root them. Oh, and the equations are missing a factor of 2.

 

[Popz]

Thank you! I had an attempt following what you said. It would be great if you could double-check if I'm on the right track as it has truly been a while since I last have done this kind of maths.

So I labeled the equations accordingly and then subsituted rc in the H-Inertia equation which gave me a simpler equation for rh. If this is correct, how do I move forward? Do I substitute (I/m) for rh in the rc equation on the top right?

Also out of curiosity, is it always the case that the isotope of a molecule doesn't affect bond length?

 

[mjc123]

I have no idea what rubbish you're doing in the right hand column.

You have two equations (which you are still writing wrongly):
I_H = 2m_Cr_C² + 2m_Hr_H²
I_D = 2m_Cr_C² + 2m_Dr_H²
You can do a simple subtraction to get
I_D - I_H = 2(m_D - m_H)r_H²
and solve for r_H, and substitute back in the equation for r_C.
Note that the question asks for the bond lengths, not r_H and r_C.

 

[Popz]

Thanks!
From that on I calculated then

Which is the same as the equation I posted in the original post except that the values for D and H are swapped. Is this correct or have I overlooked something?

For rc I then come to the same conclusion as the equation in the original post too.

 

[mjc123]

The algebra is correct, but you still haven't calculated anything!

 

[Popz]

Thank you again! The algebra was the main thing I struggled with. I think I know how to continue from then on. I subbed the variables for my calculated values and accounted for the relative positions of the atoms to the centre and got values for my bond length that resemble the literature value. :)

 

[mjc123]

Well done. But I thought it was worth emphasising, for you or anyone else out there, that if an exam question asks for bond lengths, that's what it wants. You would lose marks if you got the algebra right but stopped there, or stopped at calculating the r values.