Need help with Dynamo rule applied to coil and magnet:

[2710]

Hi, (I posted this on TSR as well, but they're being a bit slow...)

Take the following setup:

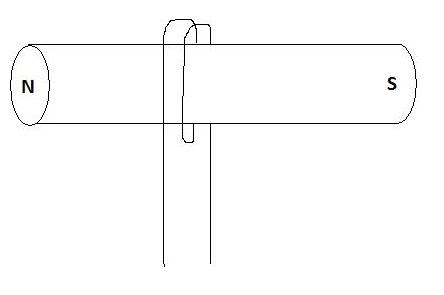
If you move the bar magnet left and right (a few cm) inside the coils, so that the ends do not leave the coil, will it induce a current/emf? I presume it does so, as I have been taught.

But I don't see why it will induce a current, since the motion in not perpendicular to the field lines. I haven't drawn the field lines in, because that would be a bit hard to do in paint lol. But I hope you can see what I mean.

Like, to induce a current, the motion of the conductor would have to CUT across a magnetic field perpendicularly. At the moment, the coils are effectively moving parallel to the magnetic field, since the magnet is being pushed left and right.

So this is basically the same diagram as above:

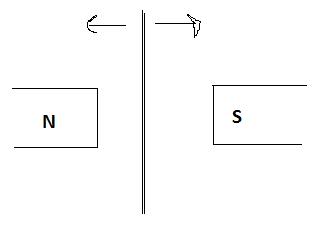
In this case, no current would be induced..right?

I know I am wrong somewhere, and I think I know where it is, but Ill let some people explain before I tell.

Thanks!

 

[Stonebridge]

There's an answer waiting for you on TSR.

 

[2710]

Ok thanks