bluecadetthree
- 2
- 0
Homework Statement
-I've attached a picture of the problem-
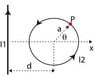
An infinitely long straight wire of steady current I1 is placed to the left of a circular wire of current I2 and radius a as shown. The center of the circular wire is distance d(≥ a) away from the straight wire. Let’s find the net magnetic (Lorentz) force acting on the entire circular wire as follows:
(A) Express the magnetic field Bp at point P (due to the
current I1) in given quantities (including its direction).
(B) The Lorentz force due to the magnetic field Bp acting on a small current segment I2dℓ at P is given by
dF = I2dℓ × Bp
Express dF = (dFx, dFy, dFz) in component representation in given quantities.
(C) By integrating your results from (B) show explicitly that the net Lorentz force for the
entire circular wire is given by
Fnet = µoI1I2\left(1-\frac{d}{\sqrt{d<sup>2</sup>-a<sup>2</sup>}}\right)\hat{&lt;b&gt;y&lt;/b&gt;}
<br />
<br />
<br />
<h2>Homework Equations</h2><br />
<br />
Most given in question.<br />
<br />
<div style="text-align: center"><b>B</b><sub>p</sub>=\frac{-μ&lt;sub&gt;0&lt;/sub&gt;I&lt;sub&gt;1&lt;/sub&gt;}{2π(d+x)}&#8203;</div><br />
<br />
<h2>The Attempt at a Solution</h2><br />
<br />
The first two parts I got through pretty easily. Part (A) was just giving the equation of the B-field for an infinite wire. For part (B) I ended up with:<br />
<br />
<div style="text-align: center">d<b>F</b>=\left(\frac{-μ&lt;sub&gt;0&lt;/sub&gt;I&lt;sub&gt;1&lt;/sub&gt;I&lt;sub&gt;2&lt;/sub&gt;acosødø}{2(d+acosø)}\right)\hat{x}+\left(\frac{-μ&lt;sub&gt;0&lt;/sub&gt;I&lt;sub&gt;1&lt;/sub&gt;I&lt;sub&gt;2&lt;/sub&gt;asinødø}{2(d+acosø)}\right)\hat{y}&#8203;</div><br />
which I got from taking the cross product of I<sub>2</sub>dl and <b>B</b><sub>p</sub>, and am fairly certain is correct.<br />
<br />
Now, for part (C) I keep getting stuck, I see what I&#039;m supposed to get for <b>F</b><sub>net</sub>, but my answer always has a natural log, or becomes zero, and I don&#039;t know how else to approach the problem.