Net Magnetic Force on Rect. Current Loop

[figs]

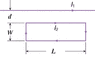
A rectangular current loop (L=0.40 m and W=0.19 m) is located near a long, straight wire (d=0.10) that carries a current of 10 A (see the drawing). The current in the loop is 20 A. The Determine the magnitude of the net magnetic force that acts on the loop.

i was chugging my B from the wire into f=IlB

 

[dextercioby]

We don't have the drawing (couldn't u attach it ?).It would make much difference how the straight conducting wire would be located wrt the rectangle...

Daniel.

 

[figs]

oops, sorry!

 

[Gamma]

You are using the correct formula. Find the force on each side of the rectangle and find the net force. You will see that the forces on the shorter sides cancels each other. So you have to consider the forces on only the longer sides of the rectangle.