Newton law's - Finding acceleration

Click For Summary

Homework Help Overview

The discussion revolves around a problem involving Newton's laws and the calculation of acceleration in a system with multiple masses connected by a string. The participants explore the dynamics of the system, particularly focusing on the acceleration of different masses and the center of mass (CM) in both inertial and non-inertial frames of reference.

Discussion Character

  • Mixed

Approaches and Questions Raised

  • Participants discuss the forces acting on each mass, including tension, weight, and normal reactions. There are attempts to derive equations based on these forces, with some questioning the assumptions made about the direction of acceleration and the role of the center of mass.

Discussion Status

The discussion is active, with participants offering various equations and approaches to understand the problem better. Some participants suggest introducing additional variables to clarify the relationships between the accelerations of the different masses. There is an ongoing exploration of how to relate the accelerations of the masses in the context of the inertial frame.

Contextual Notes

Participants note the importance of considering the inertial frame of reference for all calculations. There are discussions about the implications of the string's length remaining constant and how this affects the motion of the masses involved.

Saitama
Messages
4,244
Reaction score
93

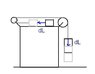
Homework Statement


(see attachment)


Homework Equations





The Attempt at a Solution


I assumed that the acceleration of 5M is towards the right and is ##a##. Moving to the frame of 5M, the other two blocks experience a pseudo force.
The forces acting on M are the tension in the string, pseudo force, its weight and the normal reaction from 5M.
##T+Ma=Ma'##
Similarly for 2M,
##2Mg-T=2Ma'##
But I still need one more equation to reach the answer.

Any help is appreciated. Thanks!
 

Attachments

  • problem.jpg
    problem.jpg
    12.7 KB · Views: 328
Physics news on Phys.org
The equation for the CM?

ehild
 
ehild said:
The equation for the CM?

ehild

[tex]a_{cm}=\frac{Ma'+2Ma'}{8M}=\frac{3a'}{8}[/tex]
Is this correct? And how does this help me? :confused:
 
Does the CM accelerate in horizontal direction in the inertial frame of reference?
By the way , I would use inertial frame for all parts.

ehild
 
ehild said:
Does the CM accelerate in horizontal direction in the inertial frame of reference?

Whoops, missed that.
[tex]a_{cm,x}=\frac{-a'}{8}[/tex]
[tex]a_{cm,y}=\frac{-a'}{4}[/tex]
I have assumed that the direction to right is positive x-axis and the direction vertically upwards is positive y-axis.

By the way , I would use inertial frame for all parts.

How will you do this using the inertial frame? I assume I will have to consider the motion of the 2M block in horizontal and vertical directions.
 
The cm accelerates in vertical direction, but is there any external horizontal force?

ehild
 
ehild said:
The cm accelerates in vertical direction, but is there any external horizontal force?

ehild

No. Do you mean I should have ##a_{cm,x}=0##? I think my expression for ##a_{cm,x}## is incorrect.
 
I mean the CM of the whole system in the inertial frame of reference.

ehild
 
ehild said:
I mean the CM of the whole system.

ehild

Sorry, I still don't get it. Can you elaborate a bit more? :)
 
  • #10
If you're not comfortable thinking about the horizontal accn of CM, you can get two more equations by introducing one more unknown, the normal reaction between 5M and 2M.
 
  • #11
You need the acceleration of the big block with respect to the ground. Of course, the acceleration is zero with respect to itself, so you can not avoid using the inertial frame of reference.

ehild
 
  • #12
haruspex said:
If you're not comfortable thinking about the horizontal accn of CM, you can get two more equations by introducing one more unknown, the normal reaction between 5M and 2M.

I have to do this in the frame fixed to 5M or inertial frame?

ehild said:
You need the acceleration of the big block with respect to the ground. Of course, the acceleration is zero with respect to itself, so you can not avoid using the inertial frame of reference.

ehild

I will make equations again for the inertial frame of reference.
For M, the forces acting on it are tension, weight & normal reaction from 5M.
##T=Ma## (I feel this is not correct)

For 2M, it performs two motions, one in horizontal and the other in vertical direction.
For horizontal direction,
##N=2Ma'## (where N is the normal reaction on 2M by 5M)
For vertical direction,
##2Mg-T=2Ma##

For 5M, it perform horizontal motion, the forces acting on 5M in the horizontal direction are the tension and the normal reaction due to 2M but how would should be the value of tension? Should it be T?
 
  • #13
The tension is the same along a single rope if the pulley has zero mass.

ehild
 
  • #14
ehild said:
The tension is the same along a single rope if the pulley has zero mass.

ehild

I should have used the proper words. I meant the direction of force of tension on 5M.
 
  • #15
Actually there are three tensional forces on the big block...
 
  • #16
ehild said:
Actually there are three tensional forces on the big block...

But I need to consider only one, the other two are in vertical direction. Right?
 
  • #17
I meant three horizontal forces of tension.
 
  • #18
ehild said:
I meant three horizontal forces of tension.

I still don't see how there are three horizontal forces of tension. :confused:
 
  • #19
Two at the left pulley and one at the right one.
 
  • #20
Pranav-Arora said:
I still don't see how there are three horizontal forces of tension. :confused:

Its all Newton's THIRD Law.

At the right pulley, there is a string passing over it. That pulley, due to strands of the string exerts a force on the big block rightwards due to Newton's third law. (Why ?) Can you find that force ?

Also, at the left pulley, there are two forces acting on the big block and they are horizontal. (Find their directions as a hint.)

Also, on observing carefully the right pulley, there is one strand of the string pushing the big block downwards. (That's Newton's third law. Do not consider that as tension.)
 
  • #21
Looks like I reached close to the answer but its still not correct.

For 5M, it performs horizontal motion, hence ##T-N=5Ma'## ...(i)
I had the following equations:
##T=Ma## ...(ii)
##2Mg-T=2Ma## ...(iii)
##N=2Ma'## ...(iv)

From (i) and (iv), ##T=7Ma'##, equating this with (ii), ##a=7a'##
From (ii), ##2Mg=3Ma \Rightarrow 2g=21a' \Rightarrow a'=2g/21## but this is incorrect. :confused:
 
  • #22
The 2M mass moves both in vertical and horizontal direction, with different accelerations.

ehild
 
  • #23
ehild said:
The 2M mass moves both in vertical and horizontal direction, with different accelerations.

ehild

Yes, I even took care of that. I expressed the vertical acceleration(a') in terms of thorizontal acceleration(a).
 
  • #24
The vertical acceleration of 2M is not the same as the horizontal acceleration of M.
 
  • #25
ehild said:
The vertical acceleration of 2M is not the same as the horizontal acceleration of M.
Why not?
 
  • #26
ehild said:
The vertical acceleration of 2M is not the same as the horizontal acceleration of M.

Then how am I going to make one more equation for that? And why they aren't same?
 
  • #27
Sammy, do you ask me? I wish Pranav to find it out. ehild
 
  • #28
Pranav-Arora said:
Then how am I going to make one more equation for that? And why they aren't same?

Why should they be the same? Remember, you are in the inertial frame of reference for all masses.
 
Last edited:
  • #29
ehild said:
Why should they be the same? Remember, you are in the inertial frame of reference for all masses.

I haven't got any idea about it but is this because of the motion of 5M?
 
  • #30
Yes.
 

Similar threads

Finding acceleration of the pulley block system
  • · Replies 23 ·
Replies
23
Views
3K
Mechanics question: Three masses and a pulley on a tabletop
  • · Replies 3 ·
Replies
3
Views
1K
Newton's laws homework: inclined plane with pulley
  • · Replies 12 ·
Replies
12
Views
1K
Tension in a supporting thread after a second supporting thread is cut
  • · Replies 16 ·
Replies
16
Views
1K
Pseudo Forces on a Mass in a Groove on a Rotating Disc
  • · Replies 5 ·
Replies
5
Views
1K
Feynman's Lectures exercise about Newton's laws
  • · Replies 13 ·
Replies
13
Views
2K
What is the initial acceleration of mass 5M in an ideal pulley system?
  • · Replies 5 ·
Replies
5
Views
4K
Newton's shell theorem - all mass is concentrated at its centre
  • · Replies 16 ·
Replies
16
Views
2K
Newton's law problem: Pushing 2 stacked blocks on a horizontal table
  • · Replies 13 ·
Replies
13
Views
3K
Newton's law problem: Helicopter lifting a box with a rope
  • · Replies 5 ·
Replies
5
Views
3K