MrLiou168
- 14
- 0
Homework Statement
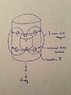
I'm trying to figure out and explanation as to why a strong magnet drops so slowly through a non-magnetic but conducting Cu tube. The attached diagram shows the original B field, induced Eddy currents, and secondary B field as a result of those Eddy currents, but I can't figure out my Force vectors. Any help greatly appreciated.
Homework Equations
F = qvB
F = qv X B
F = IL X B
The Attempt at a Solution
See attached diagram...