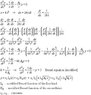Non-homogeneous differential equation

[Juliousceasor]

1. Homework Statement

I am trying to find out the soulution of the following non homogeneous differential equation with variable coefficients. The differential equation is given as follows

2. Homework Equations

y''+(1/x)y'-(A0/x)y = -B0/x

where,
A0,B0 = constants

Does anyone have any idea how to solve this one?
help is greatly appriciated..
Thanks!

 

[JJacquelin]

First consider the EDO :
y''(x) +(1/x)y'(x) -(A0/x)y(x) = 0
Let x = k t² and determine k so that the EDO be transformed into :
y''(t) +(1/t)y'(t) -y(t) = 0
which is a basic form of Bessel equation.
Then, consider the complete EDO :
y''(x) +(1/x)y'(x) -(A0/x)y(x) = -B0/x
A particular solution is obvious. Add it to the preceeding result.

 

[Juliousceasor]

I don't quite get the transformation..Could you please expand it a little bit
Thanks..

 

[JJacquelin]

A little bit more expanded ... in attachment

 

[Juliousceasor]

A little bit more expanded ... in attachment

thanks a lot..was really appriciated

 

[Juliousceasor]

I got the solution but if i want to perform simulations i need a general solution of bessel funtion of the first kind...There are 1000 different forms of this funtion available..I am a bit confused which to use?

Could you help?

 

[JJacquelin]

There are 1000 different forms of this funtion available..I am a bit confused which to use?

There is only one "Modified Bessel Function of the first kind" and order zero, which symbol is I₀.
There is only one "Modified Bessel Function of the second kind" and order zero, which symbol is K₀.
That is all what you need.

 

[Juliousceasor]

thanks mate...I couldent understand that J0 ist the 0th order..

 

[Juliousceasor]

First consider the EDO :
y''(x) +(1/x)y'(x) -(A0/x)y(x) = 0
Let x = k t² and determine k so that the EDO be transformed into :
y''(t) +(1/t)y'(t) -y(t) = 0
which is a basic form of Bessel equation.
Then, consider the complete EDO :
y''(x) +(1/x)y'(x) -(A0/x)y(x) = -B0/x
A particular solution is obvious. Add it to the preceeding result.

The perticular solution is not that obvious...As after taken general form of perticular solution as y=a*x^-1 i am getting pretty weird results..Am i doing it right?

 

[JJacquelin]

I couldent understand that J0 ist the 0th order..

Not "Oth order", but order=0
J0 is the Bessel function of the FIRST KIND and order 0. See :
http://mathworld.wolfram.com/BesselFunctionoftheFirstKind.html

 

[JJacquelin]

Hi mate !

The perticular solution is not that obvious...

y''(x) +(1/x)y'(x) -(A0/x)y(x) = -B0/x
Obviously, y(x) = B0/A0 is a particular solution.

 

[Juliousceasor]

but there is 1/x on the RHS ...what will be the general form the Particular integral...As you can see i am not so good in math..

 

[JJacquelin]

but there is 1/x on the RHS

y''(x) +(1/x)y'(x) -(A0/x)y(x) = -B0/x
Just plug y(x) = B0/A0 into the ODE
y'(x)=0 since y(x)=constant
y''(x)=0
0 + 0 -(A0/x)(B0/A0) = -B0/x
The equality in the ODE is achieved.
So, y(x) = B0/A0 is a solution of the ODE.

what will be the general form the Particular integral

It makes no sens : "general" and "particular" are contradictory and what "integral" ?

 

[cloud360]

y''(x) +(1/x)y'(x) -(A0/x)y(x) = -B0/x
Just plug y(x) = B0/A0 into the ODE
y'(x)=0 since y(x)=constant
y''(x)=0
0 + 0 -(A0/x)(B0/A0) = -B0/x
The equality in the ODE is achieved.
So, y(x) = B0/A0 is a solution of the ODE.

It makes no sens : "general" and "particular" are contradictory and what "integral" ?

i think he means Yp

y=Yc+Yp

Yc= complimentary solution
Yp=particular solution (user called it particular integral)

 

[Juliousceasor]

Yes generally in the calculus or differential equations books it is called as perticular integral..And this definition is also not so senseless..but anyways that's a million for your help..