guitar24
- 9
- 0
Hello,
I am confused as to how to transform nonlinear ODEs to linear ones by change of variables. Usually its pretty straight forward and I can do it, but this particular problem has me stumped and I don't know where to begin.
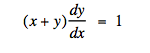
Thank you guys!
I am confused as to how to transform nonlinear ODEs to linear ones by change of variables. Usually its pretty straight forward and I can do it, but this particular problem has me stumped and I don't know where to begin.
Homework Equations
Thank you guys!