Normal Force between accelerating blocks

[disque]

Homework Statement

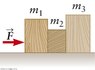
Three blocks rest on a frictionless, horizontal table (see figure below), with m1 = 8 kg and m3 = 15 kg. A horizontal force F = 104 N is applied to block 1, and the acceleration of all three blocks is found to be 3.2 m/s2.

Homework Equations

W=mg
F=ma
Normal Force=Weight (horizontal surface)

The Attempt at a Solution

First off, I had to find the mass of the second block which was just 9.5, but the second part of the problem wants me to find the normal force between blocks 2 and 3. I thought you just added the weights of the two together which gave me 240.1(240 w/ sig figs) but that was wrong. I am thinking I have to incorporate the force they gave me somewhere in the problem, the problem is just where? Please help if you have time I would appreciate it. Thanks a lot. I attached the picture given too by the way.

 

[LowlyPion]

Think of the third block in isolation?

Isn't the force on it what accelerates it at 3.2 m/s²

 

[disque]

I don't understand what you are trying to say. I realize if I just look at the third block in isolation then W would equal 147 which is the mass times g. Is that correct, and what do I do from there?

 

[disque]

Anybody know this? I am still lost.
Thanks a lot

 

[Doc Al]

I don't understand what you are trying to say. I realize if I just look at the third block in isolation then W would equal 147 which is the mass times g. Is that correct, and what do I do from there?

That's correct, but the weight is irrelevant. (The vertical forces cancel.) Consider the horizontal forces acting on the blocks.

 

[disque]

I've tried 104 and that is incorrect...?

 

[disque]

negative is incorrect as well, just thought I'd try that and no luck. :(

 

[LowlyPion]

I've tried 104 and that is incorrect...?

But 104 N is accelerating all of the masses isn't it?

What is the mass of the 3rd block? If 104 N was accelerating the 3rd block it would be going faster. But it isn't. So what force is required to accelerate the 3rd block at the same rate as all the blocks are being accelerated by the 104 N?

 

[Doc Al]

I've tried 104 and that is incorrect...?

The 104 N force acts on block 1 and accelerates the entire set of blocks (as LowlyPion explains); it does not directly act on block 3. You have to figure out the force acting on block 3 (which is the normal force from block 2). Luckily, you know its mass and acceleration and Newton's 2nd law.