Normal Force Problem: Find Contact Force b/w Sphere, Wedge A & Wall B

[rajumahtora]

Homework Statement

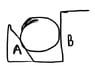
Find Normal Contact force between the sphere and wedge A and wall B.
All surfaces are frictionless and in rest.
Diagram :-

2. The attempt at a solution

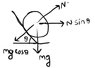
Let normal force on A be N and on B be R.
My Diagram :-

By The Diagram,
N = mgcosθ ...eq(1)
R = Nsinθ ...eq(2)
= mgcosθsinθ

But the answer if :- N = (mg)/cosθ
it is not matching with eq(1).
How is this possible?
Please help me out and explain why it is wrong

 

[Saitama]

N is not equal to mgcosθ. There is a component of R along N. Draw a separate FBD for the sphere showing the three forces.

 

[rajumahtora]

N is not equal to mgcosθ. There is a component of R along N. Draw a separate FBD for the sphere showing the three forces.

But how N is not equal to mgcosθ and is R = Nsinθ correct component

 

[Saitama]

But how N is not equal to mgcosθ and is R = Nsinθ correct component

R=Nsinθ is correct. As I said before, there is a component of R along N so you will have to take that into account while balancing the forces in the direction normal to wedge. Do you see now?

 

[rajumahtora]

N is not equal to mgcosθ. There is a component of R along N. Draw a separate FBD for the sphere showing the three forces.

But how N is not equal to mgcosθ?

 

[ehild]

But how N is not equal to mgcosθ?

R also has a component parallel to N.


Resolve N into horizontal and vertical components. The sum of all forces is zero, and that is valid to the horizontal and vertical components, separately.

ehild